Paper Information
- Title : Neural Collaborative Filtering
- Authors : Xiangnan He et al.
- Conference : WWW’17
- URL : 논문 링크
1. Introduction
개인화된 추천 시스템 (Personalized recommender system)의 핵심은 협업 필터링 (collaborative filtering) 으로 과거의 상호작용 (예: ratings, clicks)을 기반으로 아이템들에 대한 사용자의 선호도를 모델링 하는 것이다.
다양한 협업 필터링 기법 중에서 Matrix Factorization (MF)가 가장 인기 있는 기법이며, 사용자와 아이템을 shared latent space에 투영하여 latent features의 벡터를 사용해서 사용자 또는 아이템을 표현한다. 그 후에 아이템에 대한 사용자의 관심 (interaction)을 latent vectors의 내적 (inner product)로 모델링한다.
- MF가 협업 필터링에서 유명한 방법이지만, 단순한 interaction function(내적) 때문에 성능이 저해된다.
latent features을 단순하게 선형으로 결합하는 내적은 복잡한 사용자 상호작용 데이터 구조를 포착하기에 불충분하다.
따라서, 본 연구는 협업 필터링을 위한 신경망 모델링 접근법을 제안한다.
-
Implicit Feedback
Implicit feedback은 영상 시청, 물품 구매 및 아이템 클릭과 같은 행동을 통해서 사용자의 선호도를 간접적으로 반영한다.
Explicit feedback (예: 등급, 리뷰)와 비교해서 implicit feedback은 자동으로 추적될 수 있기 때문에, 더 쉽게 수집될 수 있다. 그러나, 사용자의 만족도가 관측되지 않고 negative feedback가 부족하기 때문에 활용하기는 더 어렵다.
Contribution
- 사용자와 아이템들의 latent features을 모델링하기 위한 신경망 구조를 제시하고 신경망 기반의 협업 필터링을 위한 NCF를 고안한다.
- MF가 NCF의 특수한 경우로 해석될 수 있고 다층 퍼셉트론을 활용해서 NCF 모델링에 높은 수준의 비선형성을 부여할 수 있음을 보인다.
- NCF 접근법의 효율성과 협업 필터링을 위한 딥러닝의 가능성을 증명하기 위해서 실제 데이터셋에서 실험을 진행한다.
2. Preliminaries
문제를 공식화하고 implicit feedback을 사용하는 협업 필터링을 위한 기존의 방법에 대해서 논의한다.
내적을 사용하는 경우의 한계를 강조하면서, 주로 사용되는 MF 모델에 대해서 설명한다.
2.1 Learning from Implicit Data
$M$과 $N$을 각각 사용자와 아이템의 수라고 두면, 사용자의 implicit feedback로 부터 사용자-아이템 interact matrix $\mathbf{Y} \in \mathbb{R}^{M \times N}$은 다음과 같다:
\[y_{ui} = \begin{cases} 1, & \text{if interaction (user } u\text{, item }i\text{) is ovserved;} \\ 0, & \text{otherwise.} \end{cases}\]- $y_{ui}$가 1이면, 사용자 $u$와 아이템 $i$사이에 상호작용이 있다. 하지만, 그것이 $u$가 실제로 $i$를 좋아한다는 것을 의미하지는 않는다.
-
마찬가지로, 값이 0이라는 것이 사용자 $u$가 아이템 $i$를 좋아하지 않는 것은 아니다. 단순히 사용자가 아이템을 인식하지 못한 것이라고 할 수 있다.
그렇기 때문에 implicit를 사용해서 학습하는 것이 어렵다.
- Observed entries : 최소한 아이템에 대한 사용자의 관심(interest)을 반영
- Unobserved entris : 누락된 값(missing data)일 수 있기 때문에, negative feedback이 부족하다.
Implicit feedback이 있는 추천 문제는 $\mathbf{Y}$에서 unobserved entries에 대한 점수를 추정하는 문제로 공식화된다.
모델 기반의 접근 방법을 형식적으로 표현하면 $\hat{y}_{ui} = f(u, i \mid \Theta)$로 형식화 할 수 있다.
- $\hat{y}_{ui}$: 상호작용 \(y_{ui}\)의 예측된 점수
- $\Theta$: 추정해야 하는 파라미터들
- $f$: 모델 파라미터를 예측된 점수로 맵핑하는 함수
파라미터들인 $\Theta$를 추정하기 위해서 기존의 방법들은 일반적으로 목적 함수(object function)을 최적화하는 머신 러닝 접근법을 따른다.
- pointwise loss
pointwise loss 방법은 일반적으로 \(\hat{y}_{ui}\)와 $y_{ui}$ 사이의 제곱 손실을 최소화하는 회귀 프레임워크를 따른다.
negative feedback가 Implicit feedback에는 존재하지 않기 때문에, 관측되지 않은 값은 모두 부정적인 피드백으로 처리하거나 관측되지 않은 아이템들에서 부정적인 인스턴스를 샘플링(Negative Sampling)한다.
- pairwise loss
관측된 항목들은 반드시 관측되지 않은 항목보다 높게 랭크될 것이라는 가정이 필요하다.
관측된 항목 $\hat{y}_{ui}$와 \(\hat{y}_{uj}\)의 margin을 최대화하는 방향으로 훈련한다.
=> NCF는 pointwise와 pairwise을 모두 지원한다.
2.2 Matrixcx Factorization
Matrix Factorization (MF)는 각 사용자와 아이템을 잠재 특성의 실수값 벡터로 연관짓는다.
$\mathbf{p}{u}$와 $\mathbf{q}{i}$를 각각 사용자 $u$와 사용자 $i$의 잠재 벡터라고 두면, MF는 상호작용 $y_{ui}$를 $\mathbf{p}_u$와 $\mathbf{q}_i$의 내적으로 다음과 같이 추정한다.
\[\hat{y}_{ui} = f(u, i | \mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_U^T \mathbf{q}_i = \sum_{k=1}^K p_{uk}q_{ik},\]여기서, $K$는 잠재 공간의 차원이다.
MF는 잠재 공간의 각 차원이 서로 독립이라고 가정하고 동일한 가중치로 선형적으로 결합하기 때문에, MF는 잠재 요소들의 선형모델로 보여질 수 있다.
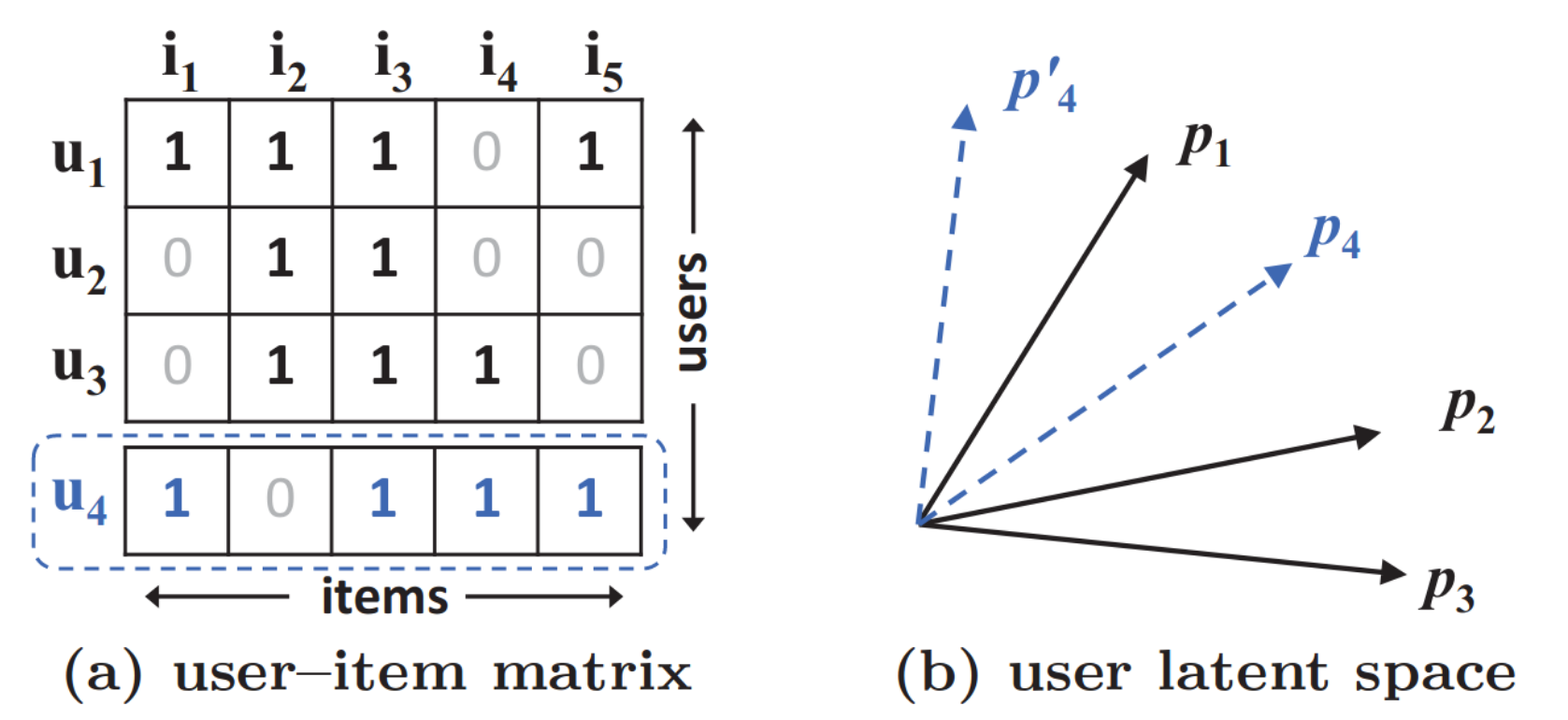
- MF는 사용자와 아이템을 동일한 잠재 공간에 매핑하기 때문에 유사성은 내적 또는 코사인으로 측정할 수 있다.
- Jaccaard 계수를 MF가 복원해야 하는 두 사용자의 ground-truth 유사도로 사용한다.
그림 1 (a)에서 $u_4$는 $u_1$와 가장 유사하고, 다음으로 $u_3$, $u_2$ 순서로 비슷하다. 하지만, (b)에서 $u_4$를 표현하는 데 이상한 부분이 보인다. 이 예시는 저차원의 잠재 공간에서 복잡한 사용자-아이템 상호작용을 추정하기 위해서 단순한 내적을 사용하여 발생하는 MF의 한계를 보여준다.
이 문제를 해결하기 위한 한 방법은 가능한 큰 $K$를 사용하는 것이지만, 이러한 희소한 환경에서는 모델의 일반화에 부정적인 효과를 줄 수 있다.
=> 본 연구에서는 DNNs를 사용하여 상호 작용 함수를 학습하여 한계를 해결하고자 한다.
3. Neural Collaborative Filtering
- 일반적인 NCF 프레임워크로 implicit data의 binary property을 강조하는 확률론적 모델(probabilistic model)로 NCF를 학습하는 방법 설명.
- MF가 NCF에 의해 표현되고 일반화될 수 있음을 보인다.
- MLP를 사용해서 사용자-아이템 상호작용 함수를 학습하도록 NCF의 인스턴스를 제안.
- 사용자-아이템 잠재 구조를 모델링하기 위해서 MF의 선형성과 MLP의 비선형성이라는 강점을 결합하는 새로운 neural matrix factorization 모델인 NCF 프레임워크를 제안.
3.1 General Framework
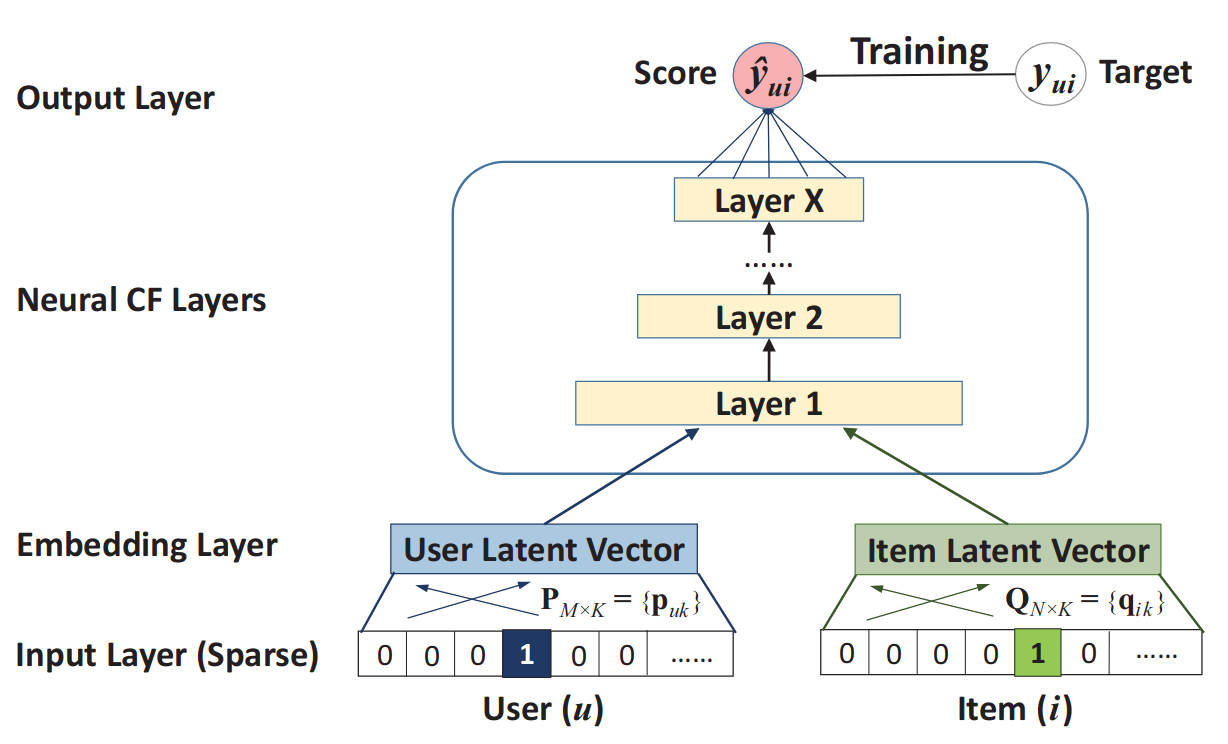
-
Input Layer (Sparse)
두 개의 특성 벡터(feature vector) $\mathbf{v}_u^\mathbf{U}$와 $\mathbf{v}_i^\mathbf{I}$는 각각 사용자 $u$와 아이템 $i$를 설명한다.
Context-aware, content-based 및 neighbor-based 등 다양한 방법으로 모델링 될 수 있지만, 본 논문에서는 단순히 원-핫 인코딩을 사용해서 이진화된 희소 벡터를 사용했다.
-
Embedding Layer
희소 표현 (sparse representation)을 dense vector로 투영하는 완전 연결 계층(fully connected layer)이다. 결과로 얻어진 사용자 (아이템) 임베딩은 latent factor model의 관점에서 사용자 (아이템)에 대한 잠재 벡터로 볼 수 있다.
이후, 잠재 벡터를 예측 점수로 매핑하는 Neural Collaborative Filtering Layers라고 불리는 multi-layer neural 구조로 사용자 임베딩과 아이템 임베딩이 공급된다.
-
Neural CF Layers
neural CF layers의 각 레이어는 사용자-아이템 상호작용의 특정 잠재 구조를 발견하도록 커스텀될 수 있다. 마지막 히든 레이어 X의 차원에 따라서 모델의 capability(용량)가 결정된다.
-
Output Layer
$\hat{y}_{ui}$와 타겟값 \(y_{ui}\) 간의 pointwise loss를 최소화하도록 훈련을 진행한다.
NCF의 예측 모델을 다음과 같이 공식화한다:
\[\hat{y}_{ui} = f(\mathbf{P}^T \mathbf{v}_u^U, \mathbf{Q}^T \mathbf{v}_i^I | \mathbf{P}, \mathbf{Q}, \Theta_f),\]- $\mathbf{P} \in \mathbb{R}^{M \times K}$: 사용자에 대한 latent factor matrix
- $\mathbf{Q} \in \mathbb{R}^{N \times K}$: 아이템에 대한 latent factor matrix
- $\Theta_f$: 상호작용 함수 $f$에 대한 모델 파라미터들
- $f$: multi-layer neural network로 정의되며, 다음과 같이 수식으로 표현한다.
- $\phi_{out}$: output layer에 대한 mapping function
- $\phi_x$: $x$번째 neural collaborative filtering (CF) layer에 대한 mapping function
3.1.1 Learning NCF
모델 파라미터를 학습하기 위해서, 기존의 pointwise 방법은 크게 제곱 오차에 대한 회귀를 수행한다.
\[L_{sqr} = \sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^-} w_{ui} (y_{ui} - \hat{y}_{ui})^2,\]- $\mathcal{Y}$: $\mathbf{Y}$에서 관측된 상호작용의 집합
- $\mathcal{Y^-}$: $\mathbf{Y}$에서 관측되지 않은 상호작용의 집합, nagative instances로 취급한다.
- $w_{ui}$: 훈련 인스턴스 $(u, i)$의 가중치를 나타내는 하이퍼파라미터
제곱 오차는 관측치가 가우시한 분포에서 생성된다고 가정한다. 하지만, Implicit data에서는 잘 맞지 않는다. 따라서, implicit data의 binary한 특성을 잘 학습할 수 있는 확률론적인 접근방법을 제시한다.
Implicit feedback의 one-class한 특성을 고려할 때, $y_{ui}$가 1이라는 것은 아이템 $i$와 사용자 $u$가 관련이 있다는 것을 의미하고, 그렇지 않다면 0을 의미한다.
-> 그렇다면 예측 점수 $\hat{y}_{ui}$는 얼마나 $i$와 $u$가 관련이 있는지를 나타낸다.
NCF에 이러한 확률론적인 설명을 추가하기 위해서, output layer에 확률론적 함수(Logistic or Probit function)을 활성화 함수로 사용해서 $[0, 1]$ 범위로 출력을 제한한다. 따라서, 다음과 같이 likelihood function을 정의한다:
\[p(\mathcal{Y}, \mathcal{Y}^- | \mathbf{P}, \mathbf{Q}. \Theta_f) = \prod_{(u,i) \in \mathcal{Y}} \hat{y}_{ui} \prod_{(u,j) \in \mathcal{Y}^-} (1 - \hat{y}_{uj}).\]likelihood의 음수 로그를 취하면 다음과 같다:
\[L = - \sum_{(u,i) \in \mathcal{Y}} \log{\hat{y}_{ui}} - \sum_{(u,i) \in \mathcal{Y}^-} \log{(1 - \hat{y}_{uj})} \\ = - \sum_{(u,i) \in \mathcal{Y} \cup \mathcal{Y}^-} y_{ui} \log{\hat{y}_{ui}} + (1-y_{ui}) \log(1-\hat{y}_{ui}).\]NCF 방법에 대해서 위의 식은 최소화해야 하는 목적 함수이며, 이것은 SGD를 사용해서 수행된다. 위의 식은 log loss라고 알려진 binary cross-entropy loss와 같다.
Nagative instance $\mathcal{Y}^-$의 경우에는, 각 반복에서 관측되지 않은 샘플에서 균일하게 샘플링하고 관측된 상호작용의 수에 대해서 샘플링 비율을 조절한다.
-> non-uniform sampling strategy가 성능을 향상시킬 수 있지만, 미래 연구로…
3.2 Generalized Matrix Factorization (GMF)
Input layer의 사용자 (아이템) ID의 원-핫 인코딩으로 얻어진 임베딩 벡터는 사용자(아이템)의 잠재 벡터로 볼 수 있다. 사용자 잠재 벡터 $\mathbf{p}_u$를 $\mathbf{P}^T \mathbf{v}_u^U$라 하고, 아이템 잠재 벡터 $\mathbf{q}_i$를 $\mathbf{Q}^T \mathbf{v}_i^I$라고 하자. 그러면 첫 번째 nueral CF layer의 매핑 함수를 다음과 같이 정의한다.
\[\phi_1 (\mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_u \circledcirc \mathbf{q}_i\]여기서, $\circledcirc$는 벡터의 element-wise product이며, 마지막 output layer의 연산은 다음과 같다.
\[\hat{y_{ui}} = a_{out}(\mathbf{h}^T(\mathbf{p}_u \circledcirc \mathbf{q}_i))\]3.3 Multi-Layer Perceptron (MLP)
NCF 프레임워크에서 MLP 모델은 다음과 같이 정의된다:
\[\mathbf{z_1 = \phi_1 (\mathbf{p}_u, \mathbf{q}_i)} = \begin{bmatrix} \mathbf{p}_u \\ \mathbf{q}_i\end{bmatrix} \\ \phi_2(\mathbf{z}_1) = a_2 (\mathbf{W}_2^T \mathbf{z}_1 + \mathbf{b}_2) \\ \cdot\cdot\cdot\cdot\cdot\cdot \\ \phi_L(\mathbf{z}_{L-1}) = a_L (\mathbf{W}_L^T \mathbf{z}_{L-1} + \mathbf{b}_L) \\ \hat{y}_{ui} = \sigma(\mathbf{h}^T \phi_L (\mathbf{z}_{L-1}))\]Activation function은 sigmoid, tanh, ReLU 중에서 ReLU를 선택한다.
NCF 모델에서는 tower structure 구조를 구현하기 위해서, 상위 레이어로 갈 수록 레이어 크기를 절반으로 줄인다.
3.4 Fusion of GMF and MLP
NCF에서는 GMF와 MLP가 동일한 임베딩 레이어를 공유하도록 한 다음 interaction function의 output을 결합했다.
\[\hat{y}_{ui} = \sigma(\mathbf{h}^T a (\mathbf{p}_u \circledcirc \mathbf{q}_i + \mathbf{W} \begin{bmatrix} \mathbf{p}_u \\ \mathbf{q}_i \end{bmatrix} + \mathbf{b}))\]이러한 경우에 GMF와 MLP는 동일한 크기의 임베딩을 사용해야 하며, 이러한 경우에는 오히려 성능의 저하를 야기할 수 있다.
따라서, NCF 모델에 더 많은 flecibility을 제공하기 위해서 GMF와 MLP는 별도의 임베딩을 학습하며, 최종 hidden layer을 연결하여 사용한다.

- $\mathbf{p}_u^G$: GMF에서의 user embedding
- $\mathbf{p}_u^M$: MLP에서의 user embedding
NCF는 user-item latent structures을 모델링 하기 위해서 MF의 linearity와 DNNs의 non-linearity을 결합한다.
3.4.1 Pre-training
NCF에서는 objective function이 non-convexity이기 때문에, gradient-based 최적화에서만 locally-optimal solution만 찾는다.
→ 따라서, GML와 MLP의 pre-trained 모델을 사용해서 NeuMF를 초기화한다.
\[\mathbf{h} \leftarrow \begin{bmatrix} \alpha \mathbf{h}^{GMF} \\ (1-\alpha) \mathbf{h}^{MLP} \end{bmatrix}\]- $\mathbf{h}^{GMF}$: pre-trained GMF의 $\mathbf{h}$ 벡터
- $\mathbf{h}^{MLP}$: pre-trained MLP의 $\mathbf{h}$ 벡터
GMF와 MLP를 훈련하기 위해서 Adam을 사용한다.
→ Adam은 SGD보다 더 빠른 convergence를 가능하게 하고, learning rate 조절에 조금 더 쉽다.
4. Experiments
RQ1: 제안한 NCF가 SOTA implicit collaborative filtering 방법보다 성능이 더 좋은가?
RQ2: 제안된 optimization framework(log loss with negative sampling)가 추천 작업에서 어떻게 작동하는가?
RQ3: hidden layer가 더 깊어지면, user-item interaction data에서 learning에 도움이 되는가?
4.1 Experimental Settings
Datasets.
1.MovieLens.
최소 20개 이상의 rations가 있는 데이터만 사용한다.
원본 데이터는 explicit feedback이지만, implicit feedback로 변환하기 위해서 user가 item을 평가했는지 여부에 따라 0 또는 1로 변환하였다.
2.Pinterest.
최소 20개 이상의 상호작용이 있는 경우만 사용했다.
각 상호작용은 user가 image를 자신의 보드에 pinned 했는지 여부를 나타낸다.
Evaluation Protocols.
- leave-ont-out
: 가장 최신 데이터를 test data로 사용하고, 나머지 데이터를 train data로 활용.
- Negative Sampling
: user와 interactive가 없는 무작위 100개의 아이템을 추출하여 순위를 매기는 방법.
성능 평가를 위한 지표로는 Hit Rate (HR)와 Normalized Discounted Cumulative Gain (NDCG)를 사용.
→ 모두 10개의 ranked list에 대해서 성능을 평가하며, 최종적으로 각 지표에 대한 평균 점수를 사용한다.
Baselines.
- ItemPop
: Item의 interaction 수로 평가하는 인기도에 따라 순위를 매김. → 대표적인 non-personalized 방법.
- ItemKNN
: 가장 기본적인 item-based callaborative filtering 방법.
- BPR
: Implicit feedback에서 학습이 가능한 pairwise ranking loss를 사용하는 방법.
- eALS
: Item recommendation을 위한 SOTA MF 방법. → WMF보다 우수한 성능을 보임.
Parameter Settings.
- 모델의 최적화를 위해서 식(7)을 사용.
- 파마미터는 평균이 1이고 표준편차가 0.01인 정규분포로 초기화하고, mini-batch Adam을 사용해서 최적화를 진행.
- Batch size: [128, 256, 512, 1024]
- Learning Rate: [0.0001, 0.0005, 0.001, 0.005]
- Last hidden layer of NCF: [8, 16, 32, 64] → Model의 capability을 결정.
- 3개의 hidden layer을 사용 [32→16→8], Embedding size는 16
- NeuMF의 $\alpha$는 0.5로 설정해서, GMF와 MLP가 NeuMF에 동일하게 기여한다.
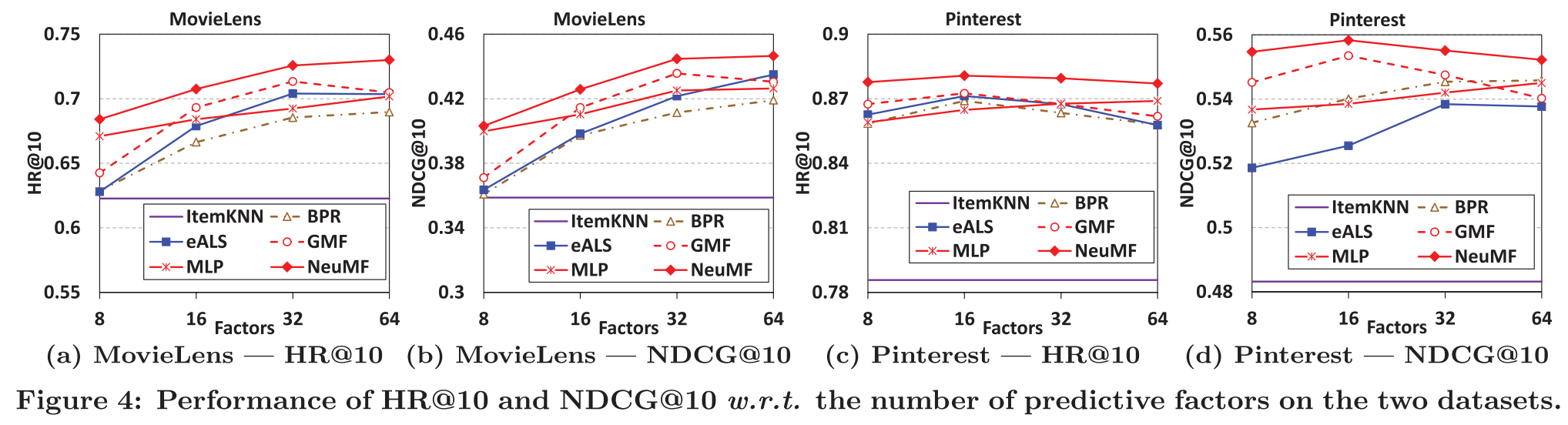
4.2 Performance Comparison (RQ1)
-
NeuMF가 다른 모델들과 비교해서 성능이 가장 우수하다.
-
NCF를 구성하는 MLP와 GMF의 성능도 상당히 우수하다.
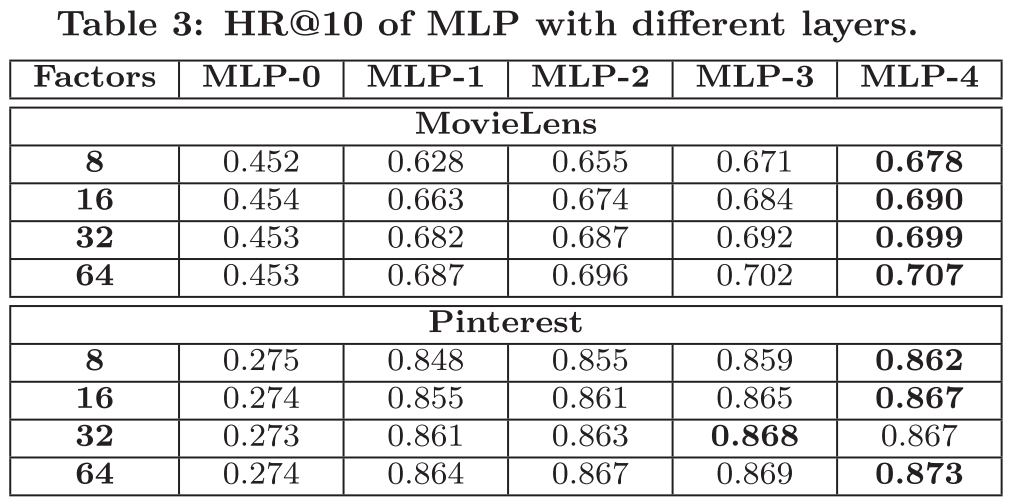
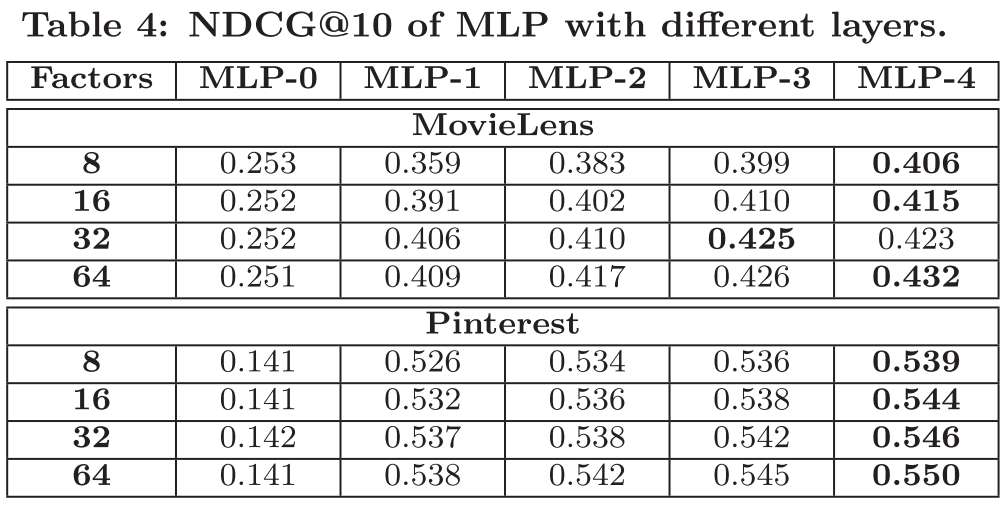
특히, MLP의 경우에는 hidden layer을 추가하면 성능이 향상될 수 있다.
-
GMF는 BPR에 비해 성능이 우수. → log loss의 효율성을 증명한다.
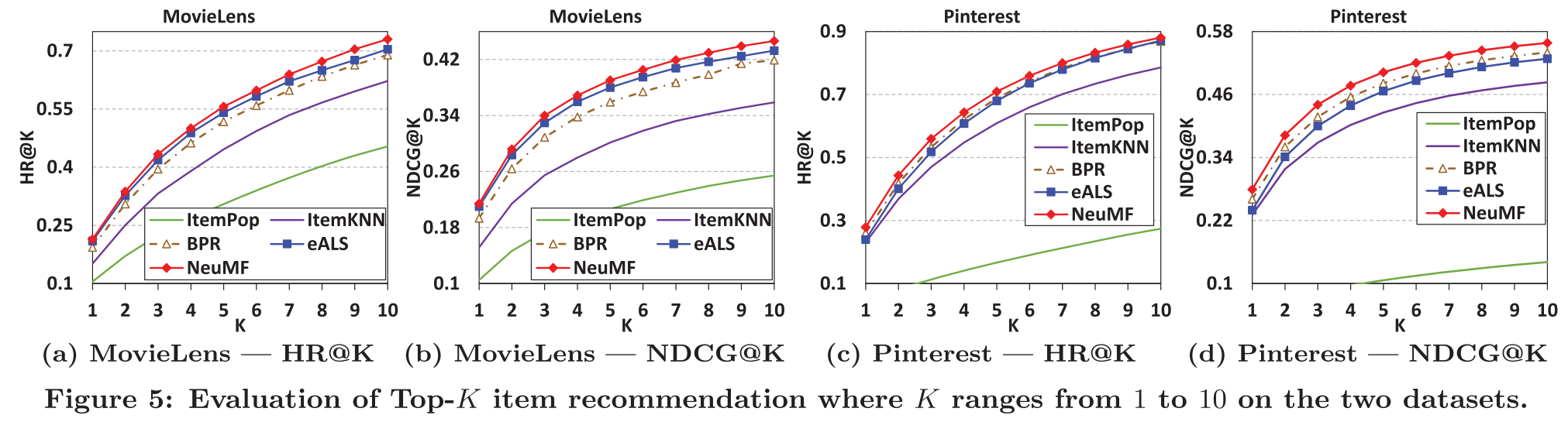
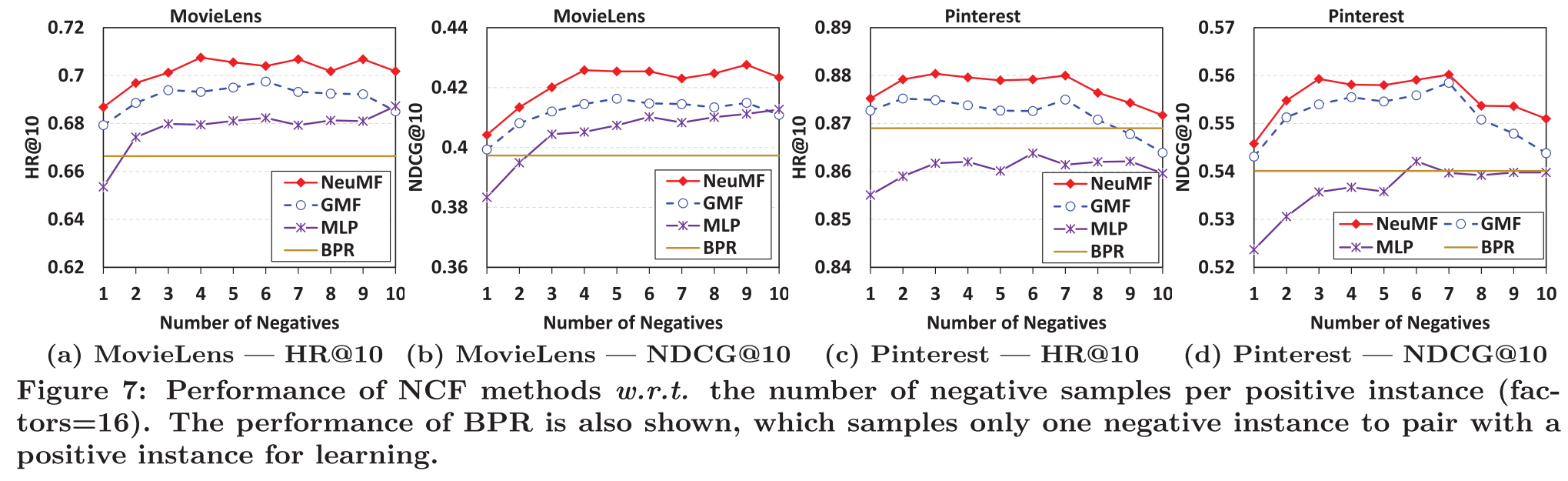
$K$가 1부터 10까지인 경우에서 top-K에서의 성능을 보여준다.
NeuMF 방법은 $K$가 증가할수록 성능이 일관되게 증가한다.
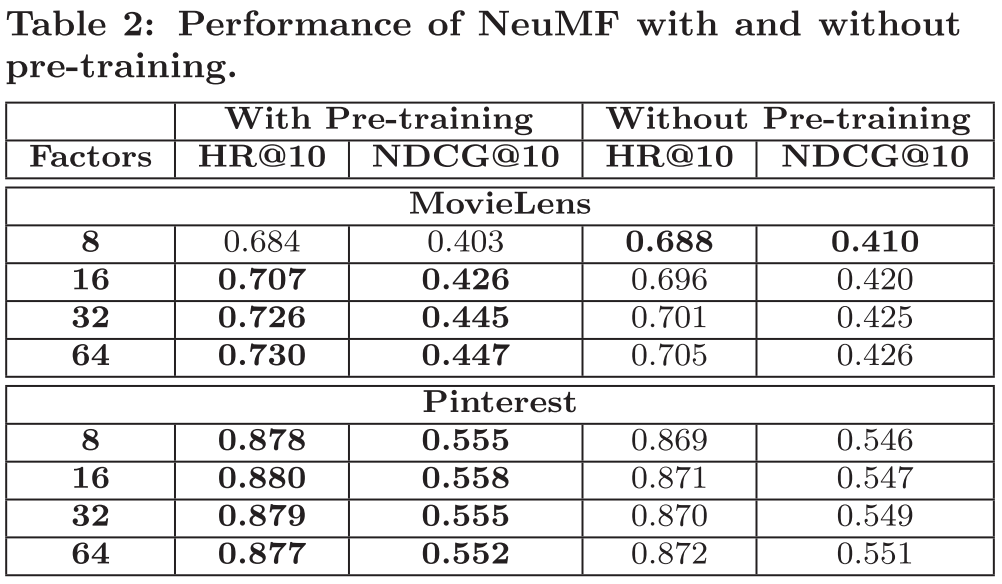
4.2.1 Utility of Pre-training
Pre-trained가 수행된 경우와 아닌 경우를 비교했을 때, Pre-training을 진행한 결우의 성능이 대부분 더 우수하다.
→ NeuMF 초기화를 위해서 pre-training 방법의 유용성을 증명한다.
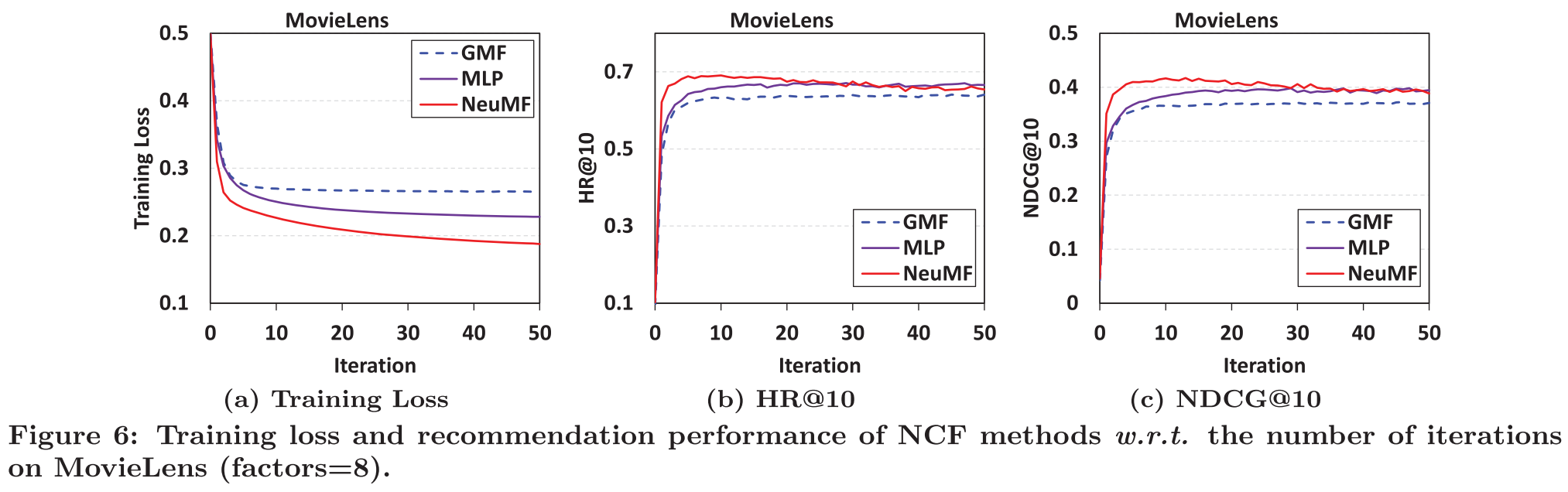
4.3 Log Loss with Negative Sampling (RQ2)
1.훈련을 반복할수록, NCF의 training loss가 감소하고 추천의 성능이 증가한다.
→ 가장 적합한 훈련 반복 횟수는 10회이며, 훈련이 더 진행되면 과적합의 위험이 있다.
2.3 가지의 NCF 방법 중에서 NeuMF의 training loss가 가장 낮으며, 가장 좋은 추천 성능을 보인다.
- Point-wise log loss는 Pair-wise log loss에 비해서 negative sampling에 대해서 sampling ratio가 flexible하다.
→ pair-wise는 하나의 negative instance만 positive instance와 paired지만, point는 조금 더 flexible하다.
4.4 Is Deep Learning Helpful? (RQ3)
-> 대부분의 경우에는 hidden layers의 갯수가 더 많을수록 성능이 향상된다.
My Opinion
최근 NCF와 MF를 비교하는 논문들을 자주 접하면서, NCF를 다시 읽어보는 기회를 가졌다.
또한 최근 GAN에 관련된 프로젝트를 진행하면서 GAN 논문을 많이 읽고 있는데, 추천 시스템의 모델 구조가 다른 분야에서 보다는 많이 단순하다는 것을 다시 느끼는 기회가 되었다.
NCF논문을 시작으로 추천 시스템의 논문들을 리뷰 할 예정으로 이후는 그래프 구조로 넘어가서 GCN, GraphSAGE, LightGCN까지 다양한 그래프 구조의 추천 시스템 모델의 논문을 포스팅 할 예정이다.