눈문 리뷰 - NGCF (Neural Graph Collaborative Filtering)

Paper Information

Title : Neural Graph Collaborative Filtering
Authors : Xiang Wang et al.
Journal : SIGIR’19
URL : 논문 링크

Introduction

협업 필터링 (CF, Collaborative Filtering) 모델을 학습하는 것은 크게 1) embedding과 2) interaction modeling 파트가 있습니다.

embedding는 user와 item을 벡터화된 표현으로 변환하는 것이며, interaction modeling은 embedding을 기반으로 과거 interaction을 복원하는 것입니다.

유명한 CF 방법으로는 MF (Matrix Factorization) 및 NeuMF (Neural Collaborative Filtering) 등이 있지만, 해당 방법들의 user-item interaction의 Collaborative Signal을 찾기에는 embedding function 부족하기 때문이다.

따라서, 본 논문에서는 그래프 구조에서 collaborative signal을 인코딩하기 위해서 사용되는 user-item interaction의 High-order connectivity을 활용해서 문제를 해결하고자 하였다.

자세한 모델에 대한 설명을 진행하기 전에, high-order connectivity에 대해서 간단히 살펴보고 넘어가자.

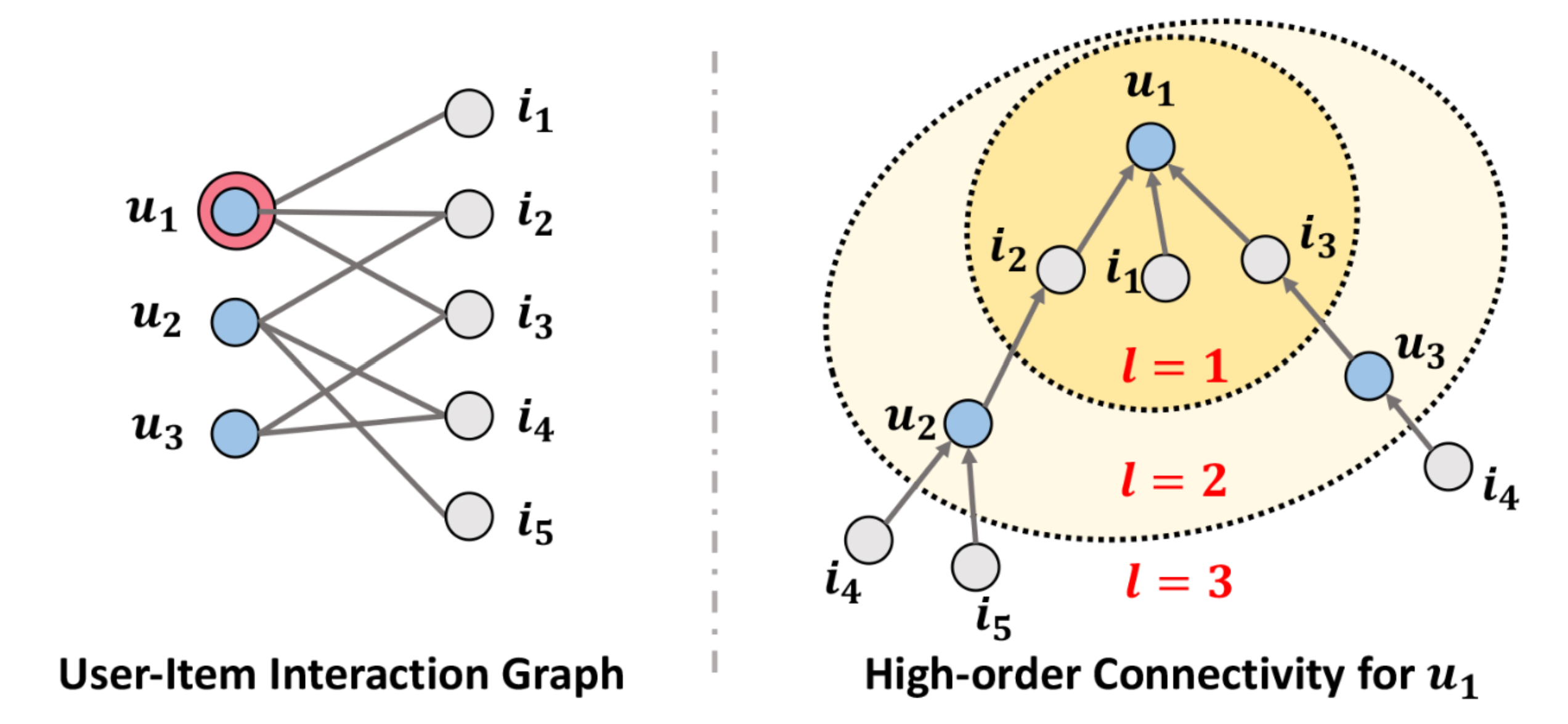
보통의 user-item interaction graph는 왼쪽의 그림처럼 구성되어 있으며 user와 item이 직접 연결되어있지 않는 Bipartite graph이다. 여기서 high-order connectivity을 설명하기 위해서 $u_1$을 중심으로 트리 구조로 변환하여 시각화하였다.

오른쪽 그림에서 $l$은 path length로 중심 노드($u_1$)에서의 거리를 의미한다. user-item interaction은 bipartite graph이므로 $l$이 홀수 인 경우에는 item node를 짝수인 경우에는 user node만 나타날 수 있다.

$l=1$인 경우에는 사용자 $u_1$과 interaction이 있는 items $i_2, i_1, i_3$에 대한 정보를 얻을 수 있으며, $l=2$인 경우에는 $l=1$의 정보를 포함해서 $u_1$과 interaction이 있었던 아이템들과 interaction이 있었던 다른 사용자들에 대한 정보를 포함할 수 있다.

저자들은 이렇게 high-order connectivity을 embedding function에 모델링 할 수 있도록 기존의 embedding propagation layer을 활용한 Neural Graph Collaborative Filtering (NGCF)를 제안했다.

NGCF에서는 embedding propagation layer을 여러 개 쌓음으로써, high-order connectivities의 collaborative filtering을 찾아내서 embedding을 강화하도록 하였다.

Methodology

NGCF는 다음 그림과 같이 크게 3가지 부분으로 구성된다.

1) Embedding layer

2) Multiple embedding propagation layers

3) Prediction layer

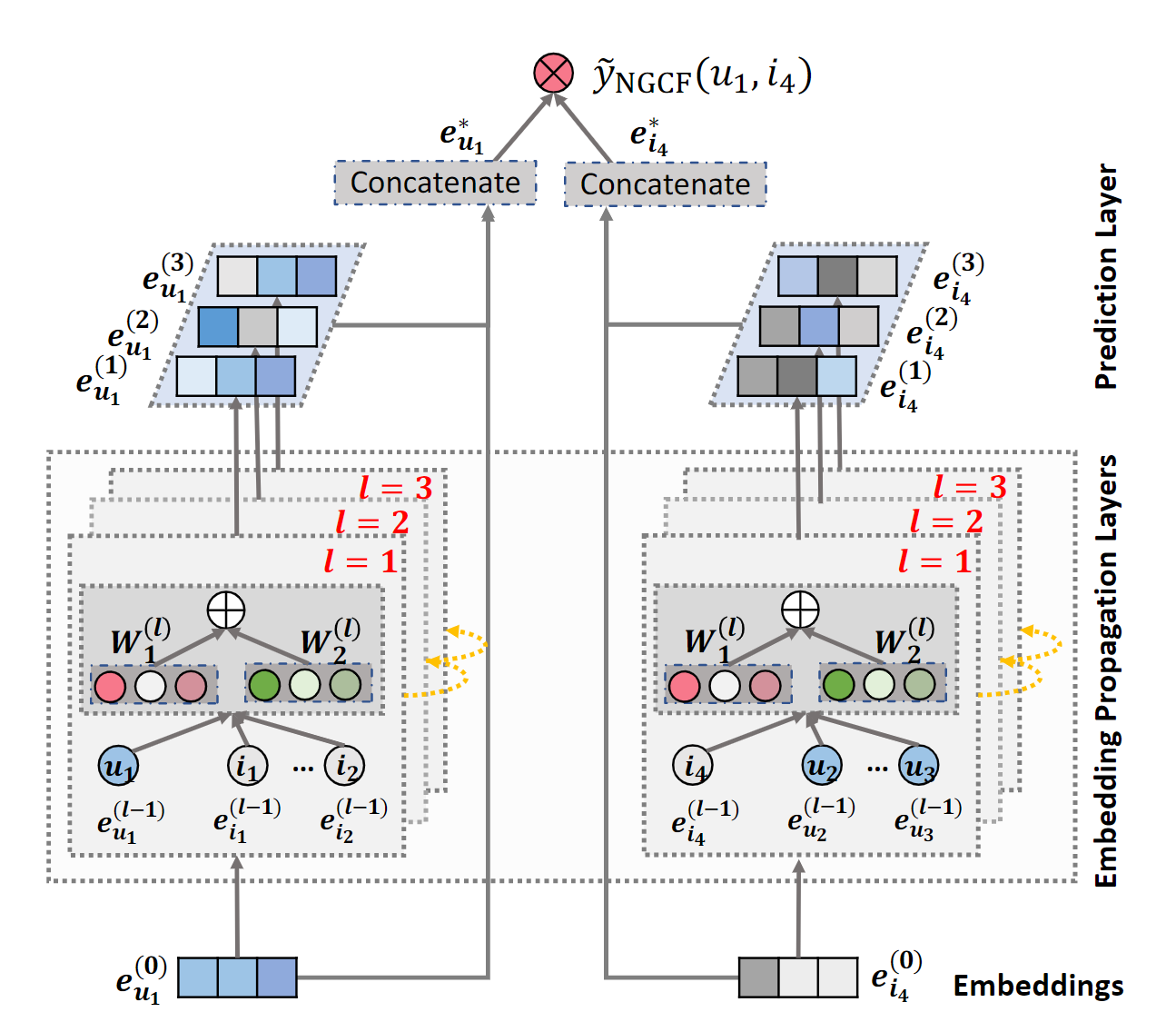
Embedding Layer

Embedding layer에서는 다른 추천 모델들에서 주로 사용되는 방법을 채택했다. 사용자 $u$의 embedding vector을 $\mathbf{e}_u \in \mathbb{R}^d$라 하고, 아이템 $i$의 embedding vector을 $\mathbf{e}_i \in \mathbb{R}^d$라 한다. 여기서, $d$는 embedding size이다.

그렇다면, 최종 embedding look-up table는 다음과 같다:

\[\mathbf{E} = [\underbrace{\mathbf{e}_{u_1}, \cdots \mathbf{e}_{u_N}}_{\text{user embeddings}}, \underbrace{\mathbf{e}_{i_1}, \cdots, \mathbf{e}_{i_M}}_{\text{item embeddings}}]\]

MF나 NeuMF에서는 해당 임베딩을 바로 interaction layer의 input으로 사용한다.

→ NGCF에서는 embedding propagation layer에서 high-order connectivity을 추가한 뒤 interaction layer로 전달한다.

Embedding Propagation Layers

Graph Neural Networks (GNNs)에서 사용되는 message-passing을 사용해서 CF signal을 capture하는 것을 목적으로 하는 파트입니다.

First-order Propagation

가정) Interacted item은 user의 preference의 근거로 작용한다.

→ 아이템을 interaction 한 user는 item의 feature로 간주되고, 이것을 근거로 두 item 간의 similiarity 계산이 가능하게 됩니다.

Message Construction

\[\mathbf{m}_{u \leftarrow i} = f(\mathbf{e}_i, \mathbf{e}_u, \mathbf{p}_{ui})\]

$\mathbf{m}_{u \leftarrow i}$: message embedding
$f(\cdot)$: message encoding function

$f(\cdot)$는 $\mathbf{e}$_$i$와 $\mathbf{e}$_$u$를 input으로 사용하고, Edge $(u,i)$의 각 propagation의 decay factor를 제어하기 위한 $p_{ui}$를 coefficient로 사용합니다.

NGCF에서는 $f(\cdot)$를 다음과 같이 설정합니다:

\[\mathbf{m}_{u \leftarrow i} = \frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}(\mathbf{W}_1 \mathbf{e}_i + \mathbf{W}_2 (\mathbf{e}_i \circledcirc \mathbf{e}_u))\]

$\mathbf{W}_1, \mathbf{W}_2 \in \mathbb{R}^{d’ \times d}$: 훈련 가능한 가중치 행렬
$\circledcirc$: element-wise product

Element-wise product는 단순히 $\mathbf{e}_i$만 반영하는 것이 아니라, $\mathbf{e}_i$와 $\mathbf{e}_u$의 affinity에도 의존하도록 한다. 그 결과, 모델의 표현 능력과 추천 성능이 증가한다.

위의 식에서, $p_{ui}$는 graph Laplacian norm인 $\frac{1}{\mid \mathcal{N}_u\mid \, \mid\mathcal{N}_i \mid}$로 설정을 하였는데, 이는 표현 학습(representation learning)의 관점에서 보면 과거 item이 사용자의 preference에 얼마나 영향을 미치는지를 반영한다.

반면, message passing 관점에서 보면 path length가 증가할수록 감소하기 때문에 discount factor라고도 한다. $\mid \mathcal{N}_u \mid$와 $\mid \mathcal{N}_i \mid$는 각각 user $u$와 itme $i$의 first-hop neighbors의 수를 의미한다.

Message Aggregation

여기서는, user $u$의 neighbors에 대한 message propagation를 예시로 aggregation을 설명합니다.

\[\mathbf{e}_u = \text{LeakyReLU}(\mathbf{m}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_u} \mathbf{m}_{u \leftarrow i})\]

$\mathbf{e}_u^{(1)}$: first embedding propagation 이후에 생성되는 user $u$의 representation
LeakyReLU: 활성화 함수 (positive or small negative로 만들기 위해서 사용)
$\mathbf{m}_{u \leftarrow u}$: user $u$의 self-connection (origin feature를 유지하기 위해서 사용)

해당 과정의 목표는 first-order connectivity를 사용해서 user의 representation과 item의 representation을 연관짓는 것입니다.

High-order Propagation

이전까지의 과정은 1개의 layer에서 propagation이 진행되는 과정을 설명했는데, 이를 여러겹으로 쌓아서 $l$개의 propagation layer가 있다고 생각하면 $l$-hop neighbors로 부터 message propagation이 이루어지는데, 수식은 다음과 같습니다.

\[\mathbf{e}_u^{(u)} = \text{LeakyReLU} (\mathbf{m}_{u \leftarrow u}^{(l)} + \sum_{i \in \mathcal{N}_u} \mathbf{m}_{u \leftarrow i}^{(l)})\] \[\begin{cases} \mathbf{m}_{u \leftarrow i}^{(l)} = p_{ui} (\mathbf{W}_1^{(l)} \mathbf{e}_i^{(l-1)} + \mathbf{W}_2^{(l)} (\mathbf{e}_i^{(l-1)} \circledcirc \mathbf{e}_u^{(l)})) \\ \mathbf{m}_{u \leftarrow u}^{(l)} = \mathbf{W}_1^{(l)} \mathbf{e}_u^{(l)} \end{cases}\]

위의 과정을 통해서, CF를 representation learning process에 반영할 수 있다.

Model Prediction

총 $L$개의 propagation layer 이후에, user $u$에 대해서 다음과 같은 multiple representations를 얻을 수 있습니다.

\[\{\mathbf{e}_u^{(1)}, \cdots, \mathbf{e}_u^{(L)}\}\]

이렇게 각각의 propagation layer에서 얻어진 representation은 서로 다른 connectivity를 반영한 message를 사용하기 때문에, user의 preference에 서로 다른 부분을 강조하게 됩니다.

이를 아이템 $i$에 대해서도 동일한 과정을 가지며, concatenation을 통해서 사용자와 아이템에 대한 벡터를 생성합니다.

\[\mathbf{e}_u^* = \mathbf{e}_u^{(0)} || \cdots || \mathbf{e}_u^{(L)} \qquad \mathbf{e}_i^* = \mathbf{e}_i^{(0)} || \cdots || \mathbf{e}_i^{(L)}\]

최종적으로, 위의 벡터들의 내적을 통해서 target item에 대한 user의 preference를 계산합니다.

\[\hat{y}_{NGCF} (u,i) = {\mathbf{e}_u^*}^T \mathbf{e}_i^*\]

Optimization

observed item이 unobserved item 보다 더 높은 예측값을 할당하는 pairwise BRP loss를 사용하며, mini-batch Adam를 사용하여 최적화를 진행했습니다.

\[Loss = \sum_{(u, i, j) \in \mathcal{O}} -\ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \lambda||\Theta||_2^2\]

Message and Node Dropout

message dropout와 node dropout라는 두 가지 dropout에 대해서 실험을 진행합니다.

Message dropout: 전달되는 message를 랜덤하게 dropout합니다.

Node dropout: 특정 노드를 랜덤하게 dropout합니다. 추가로, 제거된 노드에서 출발하는 message도 drop 합니다.

Experiments

다음의 3 질문에 답변하기 위해서 실험을 진행합니다.

NGCF가 최근 CF 방법들에 비해서 어느 정도의 성능을 보여주는가?
NGCF의 하이퍼 파라미터에 따라서 성능의 변화는 어떤가?
High-order connectivity가 representations 관점에서 어떠한 이점이 있는가?

Dataset Description

Gowalla, Yelp2018, Amazon book 3개의 데이터셋을 사용하였으며, train과 test set을 80:20으로 split한 뒤 train set의 10%는 hyperparameter 튜닝을 위해서 사용했다. 추가로, negative sampling도 실시했습니다. 다음은 각 데이터셋에 대한 대략적인 정보를 보여줍니다.

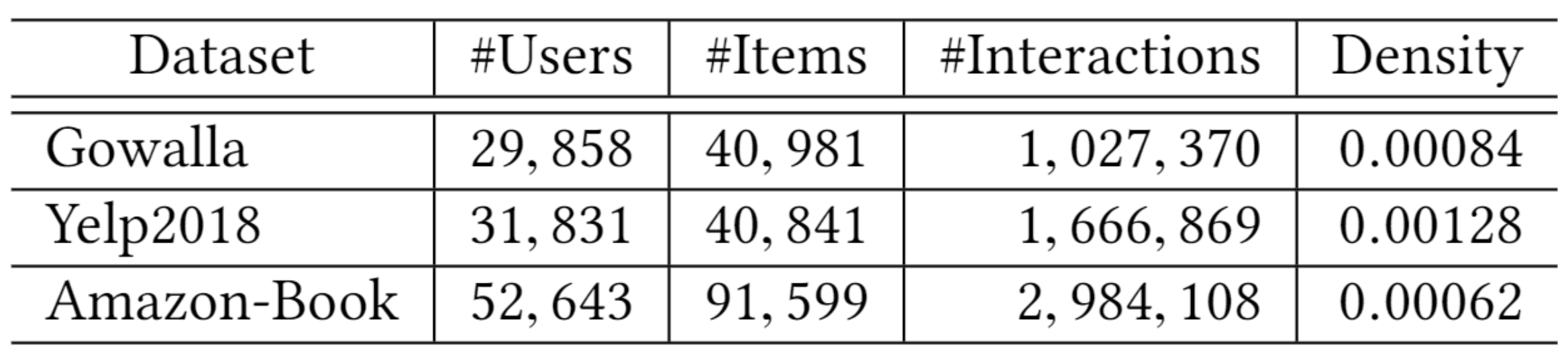
Experimental Settings

Evaluation Metrics

Top-k recommendation에 대한 성능을 측정하기 위해서 recall@K와 NDCG@K 지표를 사용했습니다. 이후, 성능 측정을 위해서 $K=20$으로 설정합니다.

Parameter Settings

모든 모델의 embedding size는 64로 통일합니다.

HOP-Rec는 random walk 방법을 사용하는 방법으로 ramdon walk로 {1, 2, 3}로 진행하며, learning rate는 {0.025, 0.020, 0.015, 0.010}으로 진행합니다.

HOP-Rec를 제외한 모든 모델에서는 batch-size가 1024인 Adam optimizer을 사용합니다. Hyperparameter는 다음에서 search를 진행합니다.

Learning rate: {0.0001, 0.0005, 0.001, 0.005}
L2 normalization: {$10^{-5}, 10^{4}, \cdots, 10^{1}, 10^{2}$}
Message droput ($p_1$): ${0.0, 0.1, \cdots, 0.8}$
Node droput ($p_1$): ${0.0, 0.1, \cdots, 0.8}$

모든 weight와 bias는 Xavier initializer를 사용해서 초기화하고, recall@20이 50epoch 동안 증가하지 않으면 종료되도록 early stopping를 사용합니다.

NGCF에서는 3-hop neighbors를 반영하도록 $L=3$으로 설정했으며, node dropout ration는 0으로, message dropout ratio는 0.1로 설정하였다.

Performance Comparison (RQ1)

Overall Comparison

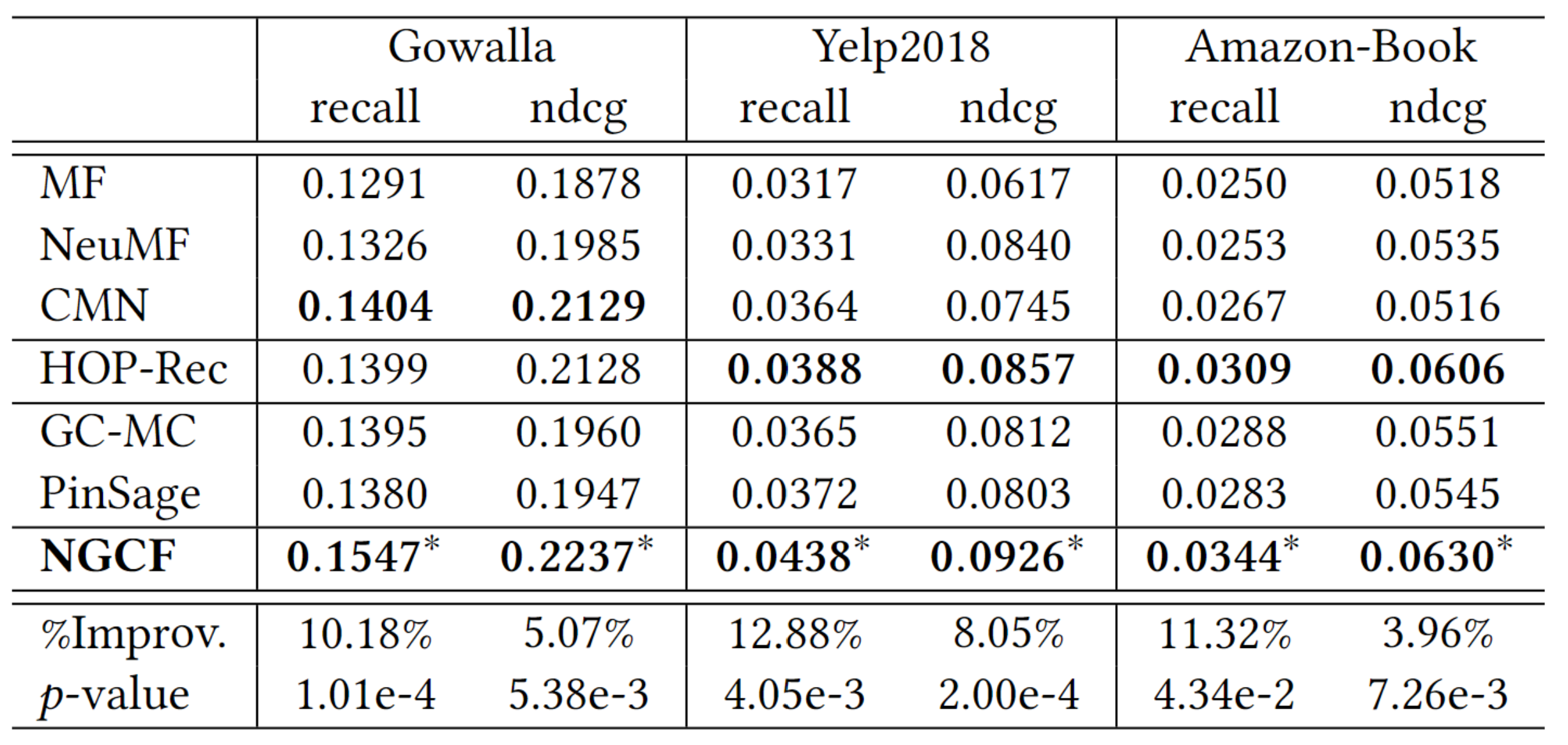
위의 표를 바탕으로 8가지로 분류해서 설명을 진행하겠습니다.

1) MF

MF 같은 경우에는 전체적으로 성능이 낮은 축에 속합니다. 이는 단순한 inner product 만으로는 user와 item의 복잡한 관계성을 포착하기에는 불충분하기 때문입니다.

2) NeuMF > MF

NeuMF가 MF보다 성능이 뛰어난 것은 바로 직전에 설명했듯이 inner product 만으로는 불충분 하기에, NeuMF에서는 user와 item의 embeddings 간의 nonlinear feature의 중요성을 강조하게 됩니다.

3) GC-MC

GC-MC는 first-order neighbor을 활용하고 있습니다. 이는 representation learning 측면에서 성능 향상이 가능합니다.

4) CMN > GC-MC

CMN과 GC-MC는 모두 first-order neighbor을 사용합니다. 하지만, CMN은 모든 이웃에 따라 가중치를 설정하는 attention mechanism을 적용합니다.

5) PinSage > CMN & HOP-Rec > CMN

PinSage와 HOP-Rec는 high-order connectivity를 활용합니다. 반면에, CMN은 first-order neighbor 만을 활용하기 때문에 성능이 차이를 보입니다.

6) NGCF

NGCF에서는 embedding propagation layer를 여러 겹 쌓음으로써, 다양한 high-order connectivity를 활용합니다. 따라서, 다른 CF 방법과 비교했을 때 우수한 성능을 보일 수 있었습니다.

7) NGCF > PinSage

PinSage도 high-order connectivity를 활용하긴 하지만, 가장 마지막 representation만 활용합니다. 반면, NGCF는 얻어진 모든 representation을 활용합니다.

여기서 알 수 있는 점은, 다른 propagation layer의 representation은 representations에서 encode하는 정보가 다르다는 것입니다.

8) NGCF > HOP-Rec

이 결과는, embedding function에서 CF의 explicit encoding을 강조합니다.

Performance Comparison w.r.t. Interaction Sparsity Levels

보통 interaction이 적은 user에게서는 high-quality representation을 얻기는 어렵습니다. 이 실험에서는 user의 interaction 수에 따라서 4개의 group로 분류하여 NGCF가 얼마나 representation을 잘 얻을 수 있는지 실험합니다. (나뉘어진 4개 그룹의 총 interaction는 같습니다.)

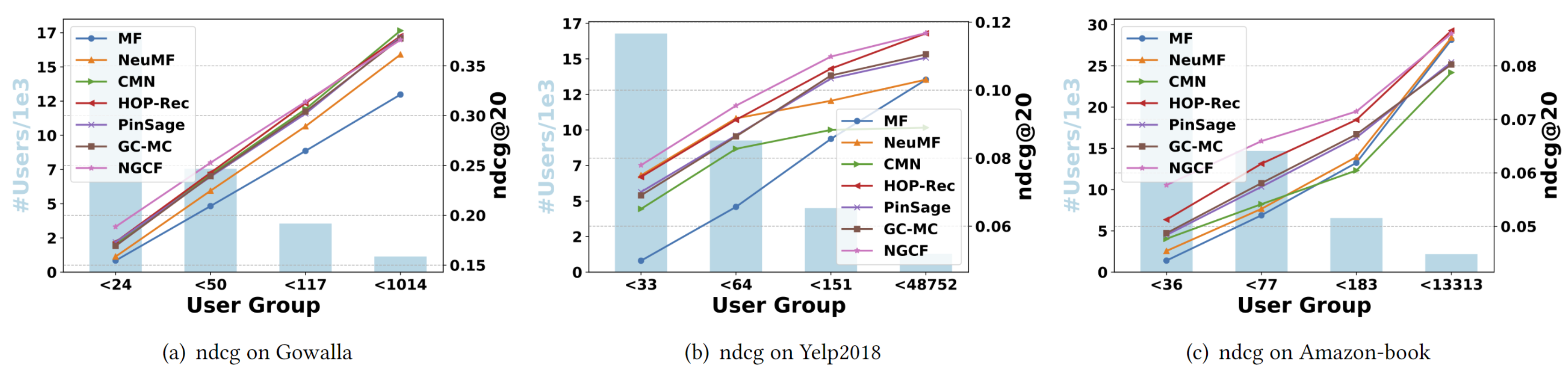
위의 결과에서 알 수 있듯이 inactive user에게서 embedding propagation이 더 유리하다는 것을 알 수 있습니다.

또한, NGCF와 HOP-Rec의 성능이 대체로 우수한 것을 알 수 있는데 이는 high-order connectivity가 collaborative signal을 포착하는데 상당히 큰 기여를 하고 있음을 알 수 있습니다.

Study of NGCF (RQ2)

Effect of Layer Numbers

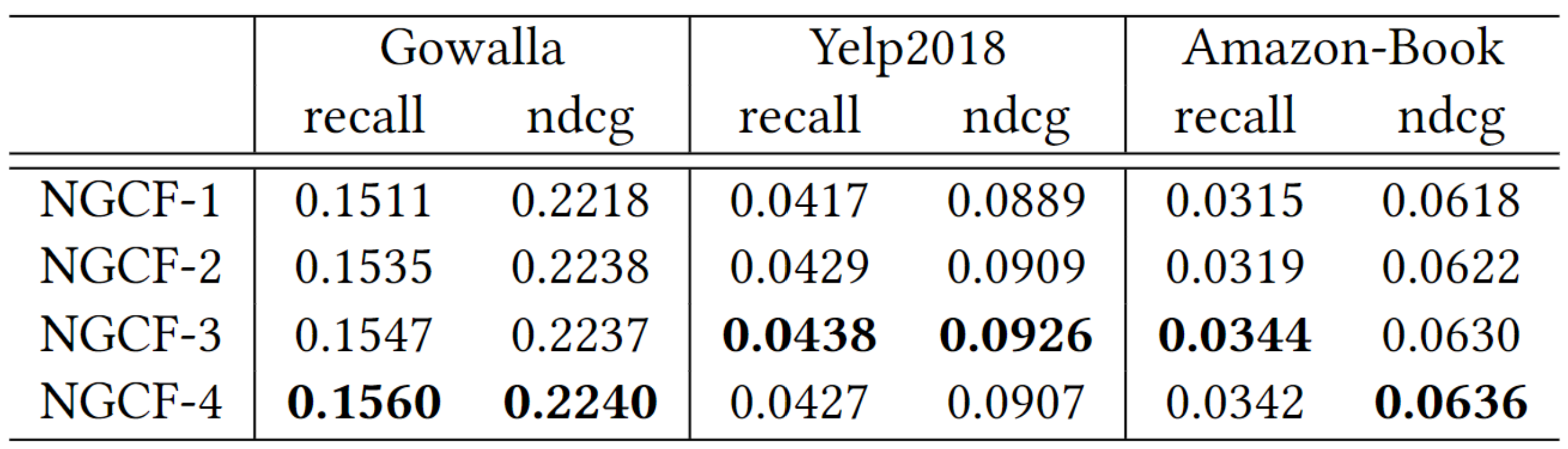
보통의 DL 방법에서 보여주는 것 처럼 NGCF도 depth가 증가할 수록 성능이 증가하는 경향을 보인다.
하지만, Yelp2018에서는 오히려 너무 깊은 구조를 적용하는 경우 representation learning에 noise를 제공하는 결과를 보여준다.
경험적으로, high-order connectivity의 explicit modeling가 추천에 한해서는 좋은 영향을 미친다.

Effect of Embedding Propagation Layer and Layer-Aggregation Mechanism

여기에서는 message function만 다르게 설정하여 모델들의 비교를 진행한다.

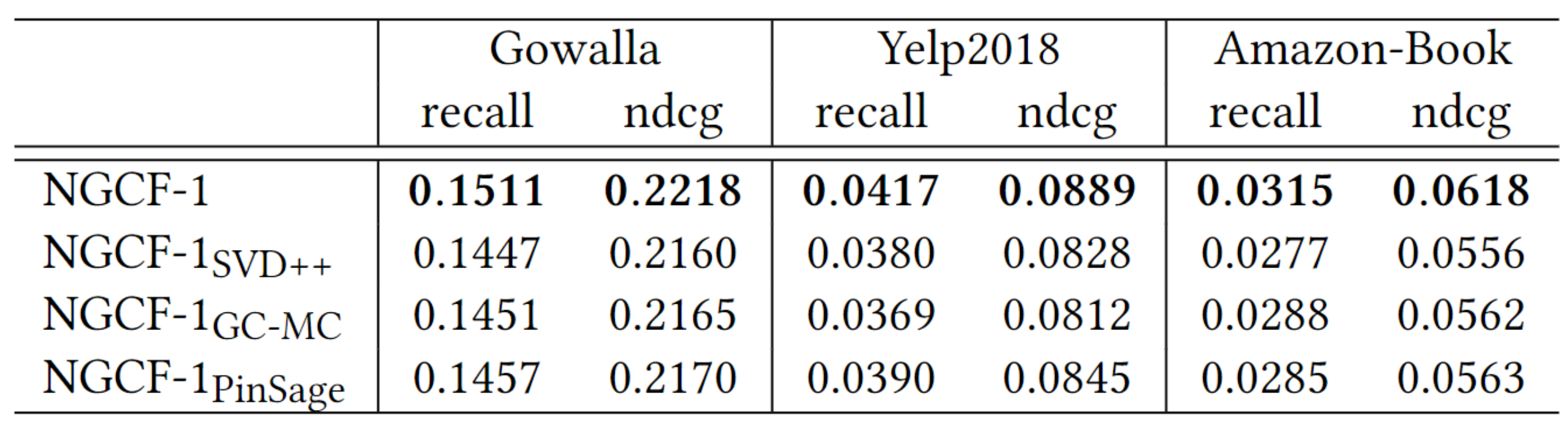
NGCF-1의 성능이 가장 우수하다. 이러한 결과의 원인은 $\mathbf{e}_i^{(l-1)} \circledcirc \mathbf{e}_u$를 통해서 $\mathbf{e}_i$와 $\mathbf{e}_u$의 affinity를 반영하기 때문이다.
NGCF-1_GC-MC와 NGCF-1_PinSage가 NGCF-1_SVD++보다 성능이 우수하다. 이는 노드 자신에 의한 message passing와 nonlinear transformation의 중요성을 강조한다.
NGCF-1_PinSage가 PinSage보다 성능이 높고 NGCF-1_GC-MC가 GC-MC보다 성능이 우수한 것은 layer-aggregation mechanism의 중요성을 강조한다.

Effect of Dropout

NGCF에서는 overtting 방지를 위해서 node dropout와 message dropout를 사용했다.

아래의 표에서 $p_1$은 message dropout ratio를 의미하고 $p_2$는 node dropout ratio를 의미한다.

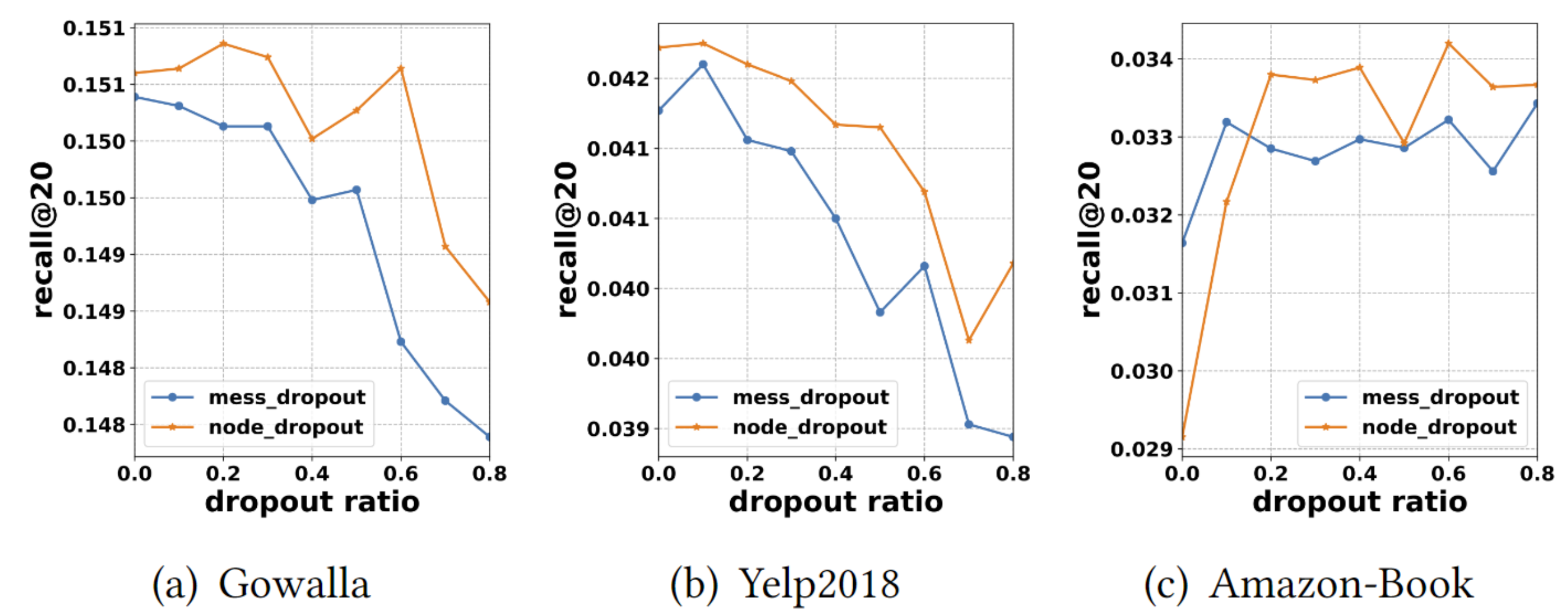
Node dropout가 Message dropout 보다 훨씬 효과적임을 알 수 있다. 이는, 특정 user 또는 item에서 나가는 message를 모두 삭제하면, 특정 edge에 대한 영향 뿐만아니라 node의 영향에도 robust한 presentation을 만들 수 있기 때문이다.

Test Performance w.r.t. Epoch

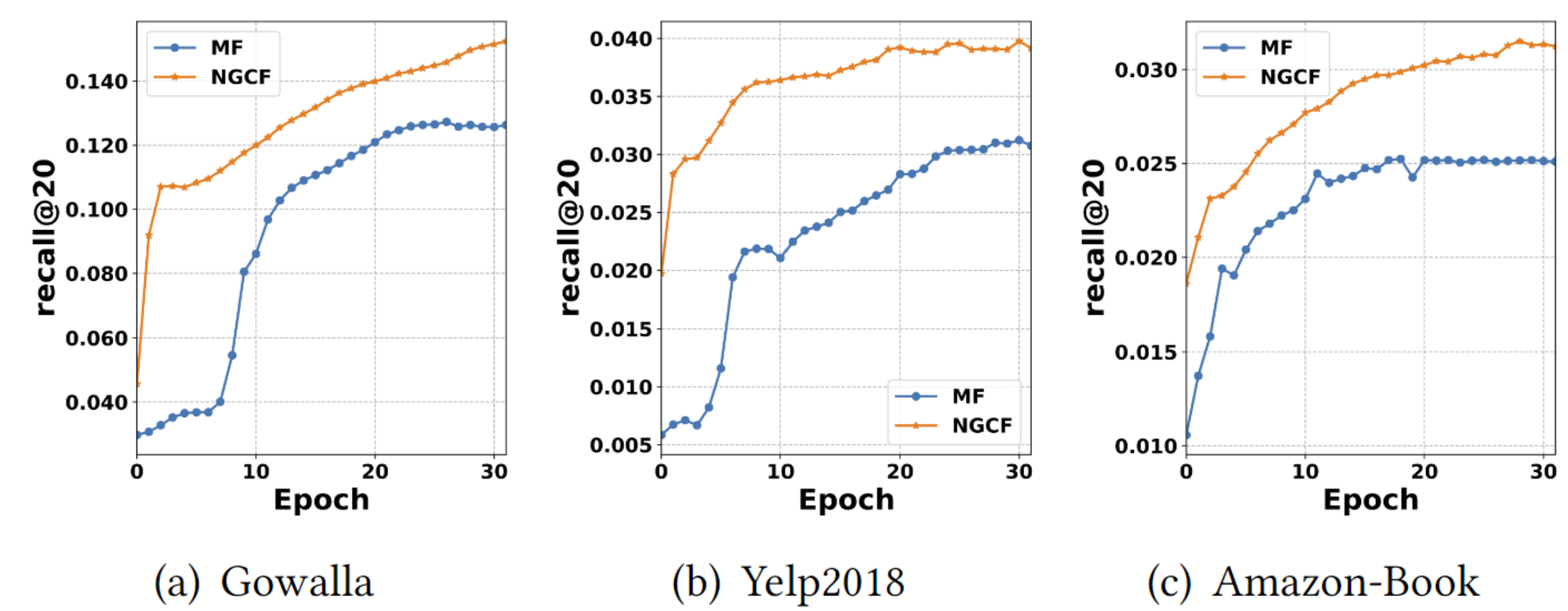
NGCF가 MF보다 빠르게 수렴함을 알 수 있다. 이는 미니 배치에서 interaction pairs를 optimizer 할 때, indirectly connected user와 item이 관련되기 때문이다.

결과적으로, NGCF의 우수한 모델 capacity와 embedding space에서 embedding propagation의 effectiveness를 입증한다.

Effect of High-order Connectivity (RQ3)

Embedding propagation layer가 embedding space에서 representation learning을 어떻게 촉진하는지 보기 위해서 실험을 진행한다.

Gowalla 데이터셋에서 무작위로 6명의 user를 추출해서 실험을 진행합니다.

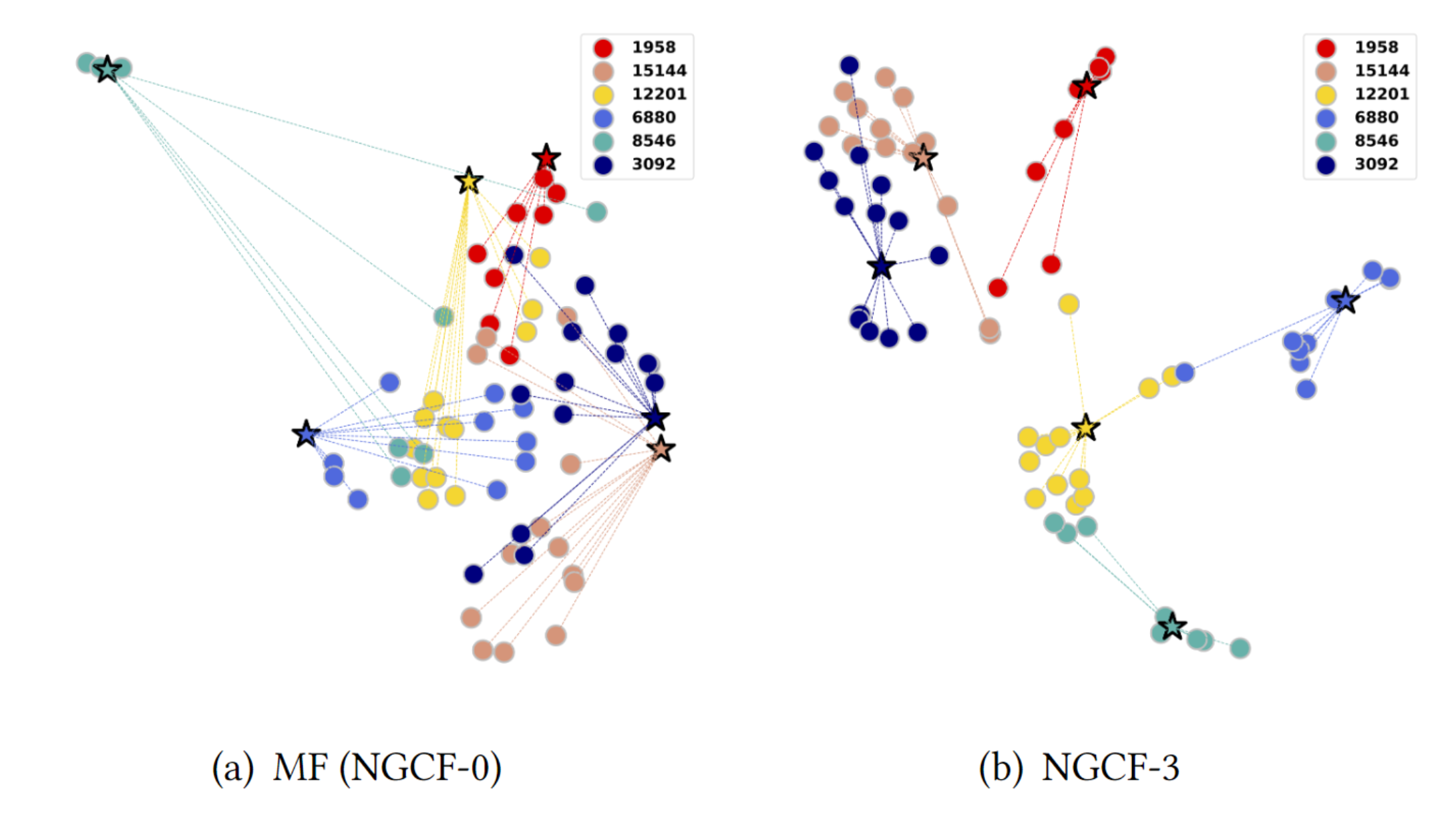
user와 item의 connectivity가 잘 반영된다는 것은 공간에서 가깝게 위치한다는 것을 의미합니다.
3개의 embedding propagation layer을 사용하는 경우 같은 색상끼리 더욱 가깝게 위치하고 있습니다.

이를 통해서, 제안된 embedding propagation layer가 collaborative signal을 더 잘 포착할 수 있음을 의미합니다.

My Opinion

3~4년 이전부터 상당히 많은 conference에서 graph 구조를 추천 task에 적용한 연구들이 발표가 많이 되고있고, accuracy 측면에서 높은 성능을 보여주고 있다. 현재까지도 graph 구조의 모델은 꾸준히 발표되고 있다. 조금 늦게 공부를 진행하고 있지만, 그래프에 대한 다양한 모델들의 논문을 읽어봐야할 것 같다.
NGCF는 이웃으로부터 message를 전달받아서 convolution이 진행된다. 이 부분을 자료구조의 graph에 맞춰서 생각하면 edge에 부여되는 값 일것 같은데, 노드 자체에 값을 부여하는 graph 모델도 있을지 궁금하다.
graph는 accuracy 측면에서 큰 성능향상을 보였는데, 평소 accuracy 만큼이나 diversity/novelty에 관심이 많아서 accuracy와 diversity/novelty를 모두 챙기려고 했던 모델이 있는지 좀 찾아봐야할 것 같다.

이전눈문 리뷰 - TADCF