Paper Information
- Title : Attention-based dynamic user modeling and Deep Collaborative filtering recommendation
- Authors : Ruiqin Wang et al.
- Journal : Expert System With Applications (2022)
- URL : 논문 링크
Introduction
협업 필터링(Collaborative Filtering) 방법은 추천 시스템에서 유명한 방법 중 하나입니다. CF에서 가장 유명한 방법은 Matrix Factorization (MF)로써 사용자와 아이템을 저차원의 공간으로 매핑한 후에 내적을 통해서 추천 결과를 생성합니다. 하지만, 해당 방법은 내적을 사용해서 계산하기 때문에 선형적인(linear) 관계만 포착할 수 있습니다.
이런 단점을 보완하기 위해서 MF에서 내적을 신경망으로 대체하는 방향으로 발전하게 되었습니다. 이러한 모델들은 비선형적인 관계와 high-order feature interaction를 포착할 수 있게되었습니다. 하지만, 신경망 구조만 사용하는 경우에는 오히려 선형적인 관계를 포착할 수 없기 때문에, 선형 및 비선형 관계를 모두 포착하기 위해서 두 가지 방법을 결합하는 NCF와 같은 모델도 소개되었습니다.
하지만, 여전이 이러한 모델들은 사용자의 취향(preference)를 모델링하기 위해서 과거 상호작용(historical interaction)을 모두 사용하기 때문에 사용자의 취향을 정적으로(static) 모델링 하게 됩니다. 쉽게 말하면, 실제 상황에서 사용자들의 취향은 시간에 따라 변화하게 되지만, 과거의 모든 상호작용을 사용하게 된다면 이를 반영할 수 없게 됩니다.
이러한 문제점들을 모두 해결하기 위해서 저자들은 time-aware attention mechanism을 사용해서 동적인 사용자 취향 (dynamic user preference)를 모델링하며, 선형 및 비선형 관계를 포착하기 위해서 두 개의 DL model을 사용하는 모델 TADCF (Time-aware Attention Deep Collaborative Filtering) 모델을 제안합니다.
Time-aware Attention-based Deep Collaborative Filtering (TADCF)
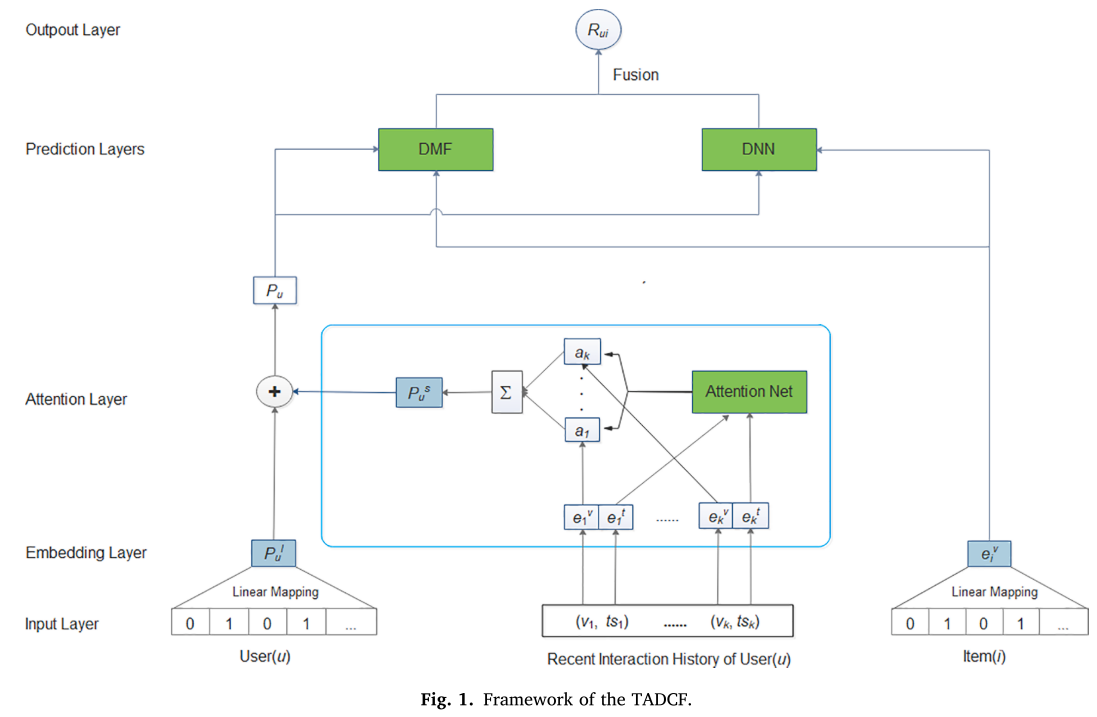
모델에 대해서 설명하기 전에 앞으로 사용될 notation은 다음과 같이 정의합니다.
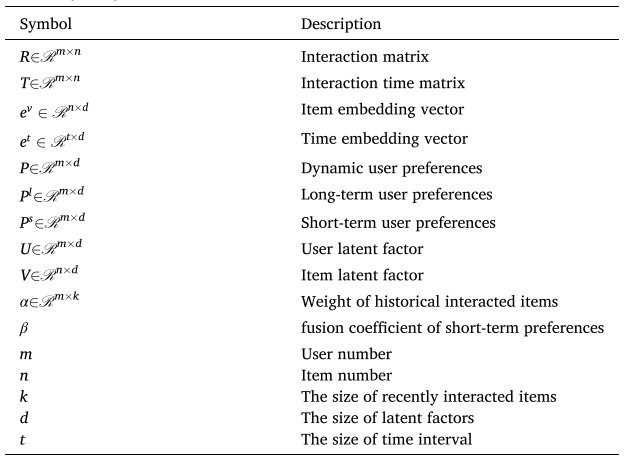
우선, 모델의 전체적인 구조는 다음과 같습니다. 이후 파트별로 나눠서 설명을 진행하도록 하겠습니다.
Embedding
CF의 embedding 기반 모델에서 가장 기본이 되는 embedding 부분 먼저 살펴보자.
먼저 아이템의 임베딩은 다음과 같이 계산된다.
\[e_j^v = W_v v_j\]여기서 $v_j$는 아이템 $j$의 implicit feedbeck (암묵적 피드백)이며, intraction matrix $j$의 $j$번째 열에 해당한다.
그런 다음, 같은 방법으로 dynamic user preferences을 위해 attention mechanism에 사용되는 시간 정보가 포함된 임베딩은 다음과 같이 계산한다.
\[e_j^t = W_t ts_j\]$W_t$는 time encoding matrix이며, $ts_j$은 아이템 $j$의 time interval으로 다음과 같이 계산한다.
\[ts_j = t_i - t_j\]$t_j$는 과거 상호작용이 있는 아이템 $j$의 intraction timestamp이고, $t_i$는 예측해야 할 아이템 $i$의 interaction timestamp이다. $t_j$와 $t_i$은 모두 interaction time matrix $T$로 부터 가져온다.
Dynamic user preference modeling
이제 이 임베딩 방법을 활용해서 dynamic user preference를 생성하는 방법을 소개한다.
dynamic user preference 위해서, short-term user preference와 long-term user preference를 구해서 두 개를 더해서 최종 user preference를 계산한다.
short-term user preference는 attention mechanism을 사용한다. attention network은 2개의 layer로 구성되며 다음과 같이 정의된다.
\[a(j) = W_2^T \phi(W_{11} e_i^v + W_{12} e_j^v + W_{13} e_j^t + b_1) + b_2\]$\phi(x) = \max(0, x)$로 ReLU 활성화 함수이다. 그런 다음, 최종 attention 가중치는 소프트맥스 정규화에 의해 다음의 식으로 계산될 수 있다.
\[a(j) = \frac{\exp(a(j))}{\sum_{l \in R_k(u)} \exp(a(l))}\]$R_k(u)$는 사용자 $u$의 최근 $k$개의 interacted items이다.
그런 다음, 임베딩 벡터들의 가중합을 통해서 short-term user preference를 구한다.
\[P_u^s = \sum_{j=1}^k a(j) \cdot e_j^v\]long-term user perence는 사용자의 과거 상호작용 아이템의 산술 평균으로 계산하며 수식은 다음과 같다.
\[P_u^I = \frac{1}{|R(u)|} \sum_{j \in R(u)} e_j^v\]- $R(u)$: 사용자 $u$가 과거에 상호작용을 했던 아이템
- $\mid R(u) \mid$: $R(u)$의 갯수
최종적으로 dynamic user preference vector은 short- and long-term preferences의 결합으로 다음과 같이 계산된다.
\[P_u = \beta \cdot P_u^s + (1 - \beta) \cdot P_u^I\]여기서, $\beta \in [0, 1]$는 결합 비율을 결정하는 hyperparameter이며, fusion coeffieient라고 한다.
DL-based feature interaction learning
지금까지 생성한 item embedding와 dynamic user preferences를 기반으로 2개의 DL-based model을 사용한다.
사용되는 DL-based models은 DMF와 DNN이 있다.
DMF Part
DMF part는 사용자와 아이템 간의 선형적인 feature를 찾아내기 위해서 사용한다.
DMF에 사용하기 위해서 dynamic user preference $P_u$와 item embedding $e_i^v$를 사용해서 사용자와 아이템의 latent presentation vectors을 다음과 같이 생성한다.
\[U_u = M_{l_1}(\phi (M_1 P_u + c_1) \cdot \cdot \cdot) + c_{l_1}\] \[V_i = N_{l_2}(\phi (N_1 e_i^v + d_1) \cdot \cdot \cdot) + d_{l_2}\]여기서, $M_\star$과 $c_\star$은 각각 사용자 모델에 대한 weight matrices와 biases이며 $N_\star$와 $d_\star$은 각각 아이템 모델에 대한 weight matrices와 biases이다. 특이한 점으로는 사용자와 아이템 모델에 대한 layer 갯수를 각각 $l_1$과 $l_2$로 설정하여 다르게 지정할 수 있다는 점이다.
이후, latent representation vectors에 내적을 사용해서 DMF Part의 결과를 도출한다.
\[y_{ui}^{DMF} = (H_u U_u) \otimes (H_v V_i)\]$\otimes$는 내적을 의미하고, $H_u$와 $H_v$는 mapping metrices로써 사용자와 아이템 벡터의 차원을 같게해주는 역할을 한다.
DNN Part
DNN Part는 DMF와는 다르게 사용자와 아이템 간의 비선형적인 features를 찾아내기 위해서 사용한다.
이전까지, 추천시스템에서 많이 사용되는 MLP 구조를 가지고 있으며 다음과 같이 연산을 진행한다.
\[y_{ui}^MLP = L_l^T \sigma (\sigma (L_1 [P_u, e_i^v] + g_1)) + g_l\]$L_\star$와 $g_\star$는 각각 모델의 weight matrices와 biases을 의미하고, $[P_u, e_i^v]$는 dynamic user preference vector $P_u$와 item embedding vector $e_i^v$의 vector concatenation를 의미한다. $l$은 layer의 갯수이다.
Fusion and learning
DMF와 DNN에서 계산된 각 결과를 합쳐서 최종 예측값을 생성한다.
\[\hat{r}_{ui} = \sigma(W_{out} [y_{ui}^{DMF}, y_{ui}^{MLP}])\]이렇게 두 개의 벡터를 결합함으로써, DMF & DNN 두 방법의 이점을 모두 취할 수 있게 된다.
해당 모델을 훈련하기 위해서 point-wise loss function류의 binary cross entropy loss를 사용한다.
\[L(\Theta) = \sum_{(u, i) \in R^+ \cup R^-} r_{ui} \log \hat{r}_{ui} + (1 - r_{ui})(1 - \log \hat{r}_{ui})\]Experiments
제안하는 모델인 TADCF를 사용해서 3가지 실험을 진행한다.
-
RQ1: TADCF가 기존의 DL-based 및 time-aware recommendation methods과 비교하여 더 나은 성능을 보이는가?
-
RQ2: 제안하는 time-aware attention mechanism이 dynamic user preference modeling에 효과가 있는가?
-
RQ3: TADCF의 각 hyperparameters가 추천 성능에 어떠한 영향을 미치는가?
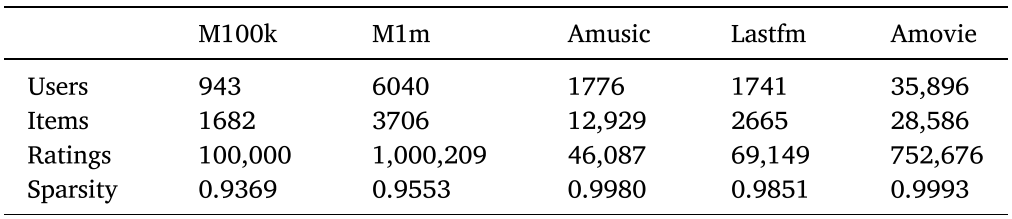
실험을 위해서 MovieLens-100k(M100k), MovieLens-1M(M1m), LastFM(Lastfm), Amazon music(Amusic), 및 Amazon movies and TV (Amovie) 데이터셋을 사용하였다.
Amusic와 Lastfm은 interaction time information이 없기 때문에 time embedding 및 time-aware attention mechanisms의 실험은 진행하지 않는다.
각 데이터셋에 대한 정보는 다음과 같다.
Implementation details
- Embedding layer: item embedding dimension 64
- Attention layer: short-term preferences을 모델링하기 위해서 사용자의 최근 20개의 interactions을 사용
- Two DNN models: item과 user의 preference을 모델링하기 위해서 dimension이 80, 40dls 2-layer DNN을 사용
- Representation learning phase: user와 item의 latent vectors을 위해서 2개의 3-layer NN을 사용하며 dimension은 128, 64, 32이다.
- Prediction layer: 4-layer MLP model을 사용하며, dimensions은 128, 64, 32, 16
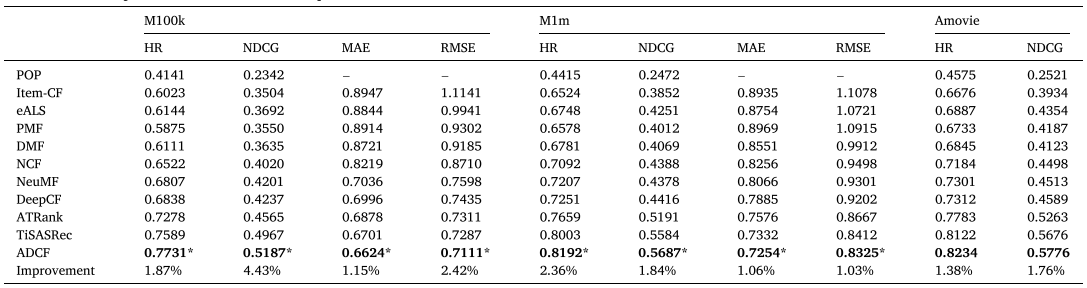
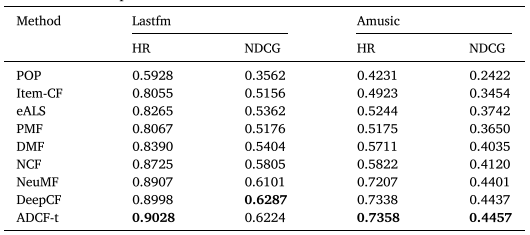
RQ1: Recommendation performance comparison
RQ2: Impacts of the Time-aware attention mechanism
- 해당 파트는 아직 명확하게 이해하지 않아서 제가 이해한대로 기술하였습니다. 띠라서, 오류가 존재할 수 있습니다.
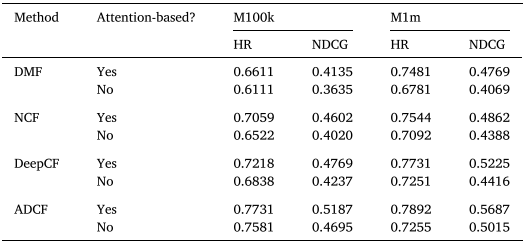
dynamic user preference을 위한 attention의 사용 여부에 대한 실험이다. 전체적으로 attention을 사용하는 경우의 성능이 더 우수하다.
- 여기서는, 8:2 train test split하는 것으로 이해하였습니다.
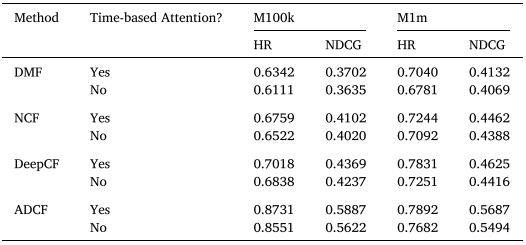
기본적인 Attention 구조에 더불어서 최근 interaction을 고려하는 경우입니다.
- 여기서는, Leave-one-out으로 최근 interaction을 고려하는 경우입니다.
종합하면, 모델 구조의 차이는 없으며 time에 대한 정보를 전체 interaction으로 볼 지 아니면, 최근 interatcion으로 볼 지 의 차이에 대한 실험인 것 같습니다.
RQ3: Sensitive analysis of hyperparameters
Hyperparameters에 대한 실험은 M1m 데이터셋에 대해서 실험을 진행했다.
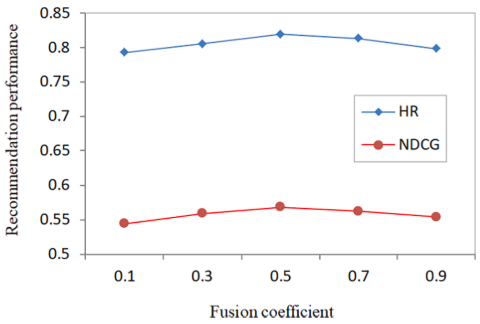
Fusion coefficient은 추천 성능에 큰 영향을 미치며, 0.5로 설정해서 short-term과 long-term을 동일하게 설정했을 때 가장 좋은 성능을 보인다. 즉, short-term을 반영하면서 long-term을 완전히 무시해서는 안된다.
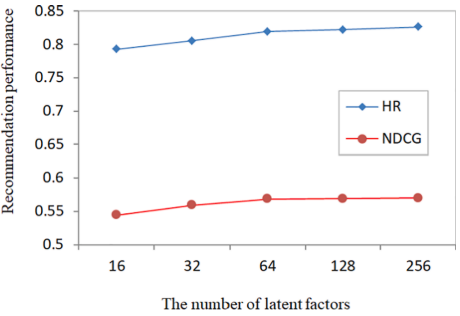
user와 item의 latent factor은 증가할수록 추천 모델의 성능은 증가한다. 하지만, latent factor이 커질수록 연산량이 증가하므로, 적절히 조율해서 64로 latent factor을 선택한다.
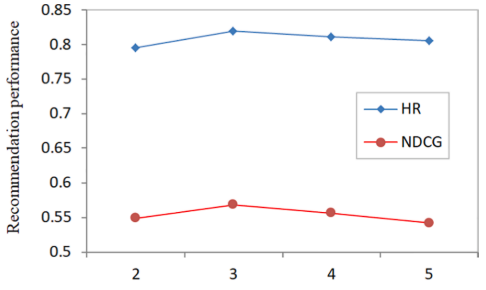
DMF에서 사용자와 아이템의 latent representation learning을 위해서 사용하는 hidden layer의 갯수에 대한 실험이다. hidden layer의 갯수가 3개일 때 최고의 성능을 보이며, 그 이후에는 오히려 성능이 감소하는 경향을 보인다.
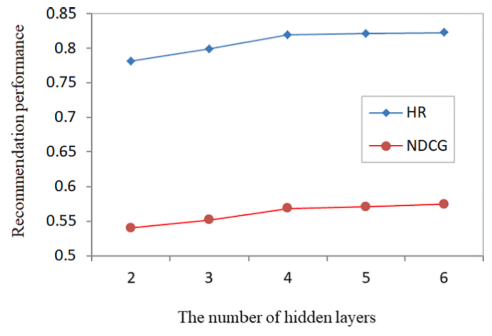
DNN에서의 hidden layer의 갯수에 대한 실험이다. hidden layer의 갯수가 많을수록 성능은 증가하지만, hidden layer의 갯수가 4개에 도달하면 더이상 눈에 띄는 향상을 보이지 않는다. 따라서 model의 hidden layer은 4개를 사용한다.
My Opinion
-
저자들이 제안한 방법이 session-based recommendation이 아니라 collaborative filtering라고 강조하였는데, 아직 session-based에 대한 지식이 없어서 정확히 어떠한 점이 있는지 잘 모르겠다… session-based에 대한 지식을 조금 더 쌓으면 해당 부분은 해결할 수 있을 것이라고 보인다.
-
CF를 키워드로 검색하다가 attention을 사용한 모델을 처음 찾게 되었는데, attention을 사용한 다른 방법도 조금 더 찾아봐야할 것 같다. 또한, attention을 사용해서 시간 정보를 CF에 결합하는 부분은 흥미로웠다.
-
RQ2에 대한 실험이 정확히 이해되지 않는 부분이있었다. Table 5의 경우 ADCF의 결과가 RQ1의 실험 결과와 일치하는 것으로 보아. Attention mechanism이 논문에서 short-term preference을 도출하는 부분일 것으로 예상된다. 하지만, 그 다음 Table 6의 time-based attention을 사용하는 경우 M100k에서 HR이 0.8731이며, 사용하지 않는 경우 0.8551로 상당히 많이 상승하였다. 해당 부분이 이해되지 않았습니다.