Paper Information
- Title : AutoRec: Autoencoders Meet Collaborative Filtering
- Authors : Sedhain Suvash et al.
- Conference : WWW’15
- URL : 논문 링크
1. Introduction
- Collaborative Filterin (CF)
: 개인화된 추천을 제공하기 위해서 아이템에 대한 사용자의 선호도에 대한 정보를 이용한다.
이번에 리뷰하는 논문은 CF 방법에 autoencoder 방법을 곁들인 AutoRec라는 새로운 모델을 제안한다.
2. The AutoRec Model
AutoRec 논문에서는 $m$명의 사용자와 $n$개의 아이템이 존재하는 rating 기반의 CF에 대해서 논한다.
- $R \in \mathbb{R}^{m \times n}$: 관측된 사용자-아이템 등급 행렬
각 사용자 $u \in U = {1 … m}$는 부분적으로 관측된 벡터 $\mathbf{r}^{(u)} = (R_{u1}, … R_{un}) \in \mathbb{R}^n$으로 나타낼 수 있으며, 아이템의 경우에도 비슷하게 각 아이템 $i \in I = {1 … n}$도 $\mathbf{r}^{(i)} = (R_{1i}, … R_{un}) \in \mathbb{R}^m$로 나타낼 수 있다.
이러한 작업의 목표는 부분적으로 관측된 $\mathbf{r}^{(i)}$ 또는 $mathbf{r}^{(u)}$를 입력으로 받아서 저차원의 잠재 공간에 투영할 수 있는 아이템 기반 또는 사용자 기반 autoencoder을 설계하는 것이다.
이후에 해당 autoencoder을 사용해서 누락된 등급을 예측하기 위해 $\mathbf{r}^{(i)}$ 또는 $mathbf{r}^{(u)}$를 재구성한다.
\[\min_\theta \sum_{\mathbb{r} \in \mathbb{S}} ||\mathbb{r} - h(\mathbb{r}; \theta)||^2_2\]여기에서 $h(\mathbb{r}; \theta)$는 입력값 $\mathbb{r} \in \mathbf{R}^d$을 재구성한 것이다.
- $f(\cdot), g(\cdot)$: Activation function
- $\theta = {\mathbb{W}, \mathbb{V}, \mu, b}$
- $\mathbb{W} \in \mathbf{R}^{d \times k}, \mathbb{V} \in \mathbb{V} \in \mathbf{R}^{k \times d}$: 변환(transformations)
- $\mu \in \mathbf{R}^k, \mathbb{b} \in \mathbf{R}^d$: 편향(bias)
위의 수식은 하나의 $k$차원 hidden layer을 가지는 auto-associative neural network에 해당하며, 파라미터 $\theta$는 backpropoagation을 통해서 학습된다.
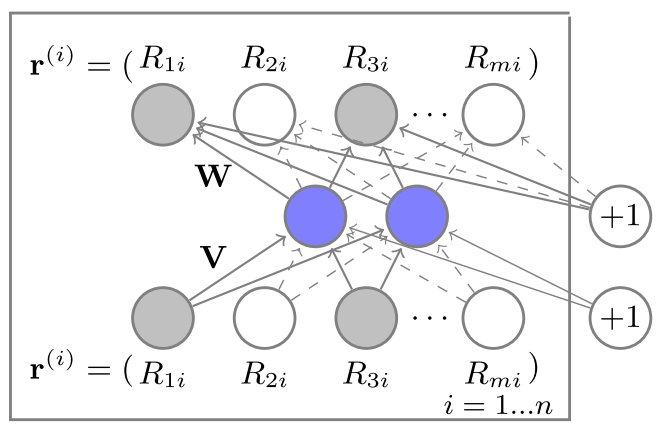
점선은 관찰된 등급에 해당하며, 일반적인 직선은 입력 $\mathbb{r}^{(i)}$에 대해서 업데이트 된 가중치에 해당한다.
정규화 강도 $\lambda > 0$에 대한 아이템 기반 AutoRec(I-AutoRec)의 objective function은 다음과 같다.
\[\min_\theta \sum_{i=1}^n ||\mathbb{r}^{(i)} - h(\mathbb{r}^{(i)}; \theta)||^2_{\mathcal{O}} + \frac{\lambda}{2} \cdot (||\mathbb{W}||^2_F + ||\mathbb{V}||^2_F)\]$ \parallel \cdot \parallel^2_{\mathcal{O}}$는 관측된 등급에 대해서만 고려한다는 의미이다.
I-AutoRec에서는 $2mk+m+k$개의 파라미터만 추정하면 된다. 학습된 파라미터 $\hat{\theta}$가 주어졌을 때, 사용자 $u$ 및 아이템 $i$에 대한 I-AutoRec의 예측된 등급은 다음과 같다.
\[\hat{R}_{ui} = (h()\mathbb{r}^{(i)}; \hat{\theta})_u\]AutoRec의 특징
- AutoRec는 autoencoder 기반의 discriminative model이다.
- AutoRec는 RMSE를 최소화하면서 파라미터를 추정한다.
- AutoRec는 훈련할 때 comparatively faster gradient-based backpropagation을 필요로 한다.
- AutoRec는 가능한 등급 $r$과 상관없이 더 적은 수의 파라미터가 필요하다. 파라미터가 적으면 AutoRec가 더 적은 메모리를 사용하며 과적합 문제에 덜 취약하다.
3. Experimental Evaluation
Baseline
- RBM-based CF model (RBM-CF)
- Biased Matrix Factorisation (BiasedMF)
- Local Low-Rank Matrix Factorisation (LLORMA)
Datasets
- Movielens 1M
- Movielens 10M
- Netflix
Experiment setting
- 데이터는 무작위로 90%-10%로 train-test 데이터를 분할한다.
- train 데이터의 10%를 파라미터 튜닝을 위해 hold-out 한다.
- 데이터 분할 절차를 5회 반복하여 평균 RMSE를 최종 결과로 사용한다.
- 모든 baselines에 대해서 정규화 강도 $ \lambda \in { 0.001, 0.01, 0.1, 1, 100, 1000 } $ 및 잠재 차원 $ k \in { 10, 20 ,40, 80, 100, 200, 300, 400, 500 } $을 사용.
- 모든 실험에는 RProp를 사용한다.
Experiment
1. item 기반과 user 기반의 RBMs와 AutoRec에 대한 성능의 비교
.png)
RBM 및 AutoRec에서 모두 사용자 기반보다는 아이템 기반 모델의 성능이 우수하다.
-> 아이템 당 평균 평점 수가 사용자당 평점보다 훨씬 많기 때문일 수 있다.
4가지 방법 중에서 I-AutoRec의 성능이 가장 우수하다.
2. 선형 및 비선형 활성화 함수 $f(\cdot), g(\cdot)$에 대해서 AutoRec의 성능의 비교
.png)
비선형을 사용하는 경우가 성능이 조금 더 우수하다. 하지만, 2개의 활성화 함수에 Sigmoid만 사용하면 오히려 성능이 나빠졌다.
이 외의 실험에서는 AutoRec는 Identity와 Sigmoid를 사용한다.
3. Hidden units의 수에 따른 AutoRec의 성능
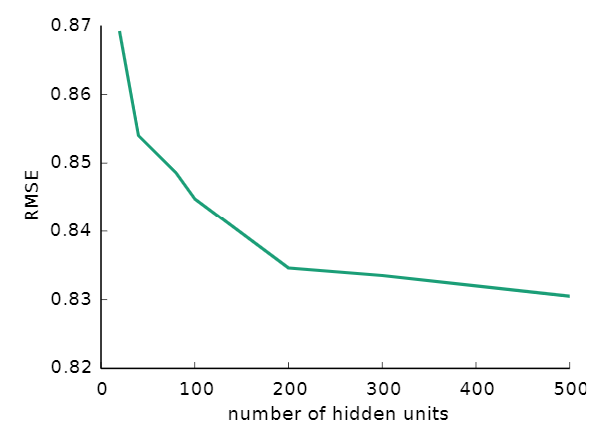
위의 그림은 hidden units의 수에 따른 AutoRec 모델의 성능의 변화를 보여준다.
Hidden units가 많으면 많을수록 성능은 증가하지만, 점차 증가폭은 감소한다.
다른 실험에서는 AutoRec의 hidden units의 갯수를 500으로 설정한다.
4. Baselines와 AutoRec의 성능 비교
.png)
Movielens 10M에서 LLORMA와 I-AutoRec의 성능이 동일한 부분을 제외하고는 모든 데이터셋에서 AutoRec의 성능이 가장 우수하다.
5. AutoRec를 더 깊게 확장할 수 있는가?
활성화 함수를 Sigmoid를 사용하고 hidden layer의 크기를 (500, 250, 500)으로 설정한 3층의 I-AutoRec으로 실험을 진행했다.
Movielens 1M에 대해서 RMSE가 0.831에서 0.827로 감소하여 AutoRec가 더 깊어지면 성능이 개선될 수 있는 가능성을 보였다.
My Opinion
대부분의 추천시스템 모델에서는 User와 Item에 대해서 Embedding vector을 input으로 사용하게 된다.
AutoRec에서 생성된 hidden units을 다른 모델에서 input으로 사용할 수 있는지 및 사용하게 되면 성능의 변화는 어떤지에 대한 실험을 진행해 보고 싶다.
기회가 된다면, 코드와 함께 블로그 포스팅을 진행하고자 한다.